Next: Method of Undetermined Coefficients Up: Linear Differential Equations Previous: Reduction of Order 目次 索引
2. Find the general solution of the following differential equations.
(a) 4th order homogeneous differential equation with the roots of the characteristic equation are
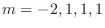
(b) 6th order homogeneous differential equation with the roots of the characteristic equation are
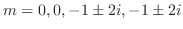
3. Solve the following initial value problems.
(a)
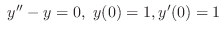
(b)
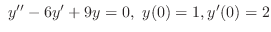
(c)
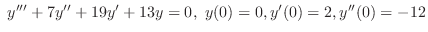
(d)
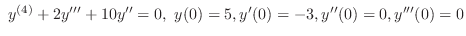
Answer
1.
(a) Let
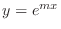 . Then we have the characteristic equation
. Then we have the characteristic equation
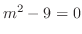 . Thus, the characteristic roots are
. Thus, the characteristic roots are 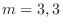 . Therefore, the fundamental solutions are
. Therefore, the fundamental solutions are
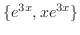
(b) Let
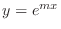 . Then we have the characteristic equation
. Then we have the characteristic equation
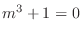 .
.
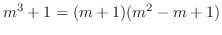
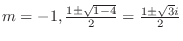 . Thus, the fundamental solutions are
. Thus, the fundamental solutions are
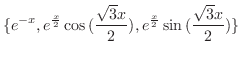
(c) Let
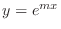 . Then we have the characterisitc equation
. Then we have the characterisitc equation
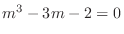 .
.
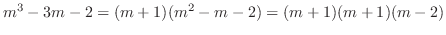
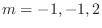 . Therefore, the fundamental solutions are
. Therefore, the fundamental solutions are
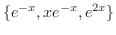
(d) Let
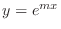 . Then we have the characteristic equation
. Then we have the characteristic equation
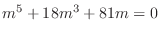 .
.
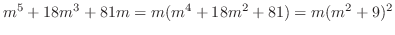
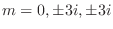 . Therefore, the fundamental solutions are
. Therefore, the fundamental solutions are
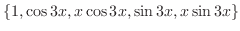
2.
(a) Let the roots of the characteristic equation be
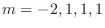 . Then the fundamental solutions are
. Then the fundamental solutions are
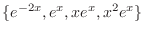
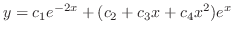
(b) Let the roots of the characteristic equation be
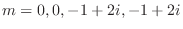 . Then the fundamental solutions are
. Then the fundamental solutions are
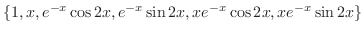
![$\displaystyle y = c_{1} + c_{2}x + e^{-x}[(c_{3} + c_{4})\cos{2x} + (c_{5} + c_{6}x)\sin{2x}] \ \ $](img787.png)
3.
(a) Let
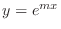 . Then we have the characteristic equation
. Then we have the characteristic equation
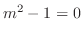 .
.
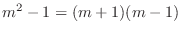
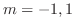 . Thus, the fundamental solutions are
. Thus, the fundamental solutions are
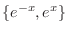
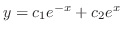
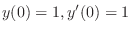 . Then
. Then
 |
 |
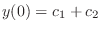 |
|
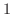 |
 |
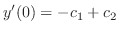 |
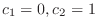 . Therefore,
. Therefore,
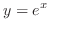
(b) Let
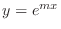 . Then we have the characteristic equation
. Then we have the characteristic equation
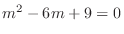 .
.
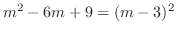
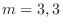 . Thus, the fundamental solutions are
. Thus, the fundamental solutions are
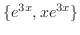
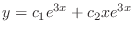
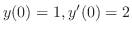 , we have
, we have
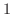 |
 |
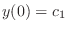 |
|
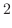 |
 |
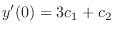 |
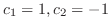 . Therefore,
. Therefore,
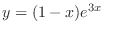
(c) Let
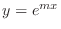 . Then we have the characteristic equation
. Then we have the characteristic equation
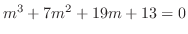 .
.
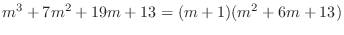
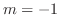 and
and
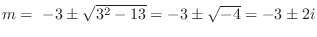 . Thus, the general solutions are
. Thus, the general solutions are
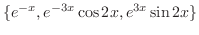
![$\displaystyle y = c_{1}e^{-x} + e^{-3x}[c_{2}\cos{2x} + c_{3}\sin{2x}] $](img813.png)
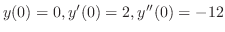 and
and
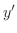 |
 |
![$\displaystyle -c_{1}e^{-x} -3e^{-3x}[c_{2}\cos{2x} + c_{3}\sin{2x}]$](img815.png) |
|
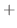 |
![$\displaystyle e^{-3x}[-2c_{2}\sin{2x} + 2c_{3}\cos{2x}]$](img817.png) |
||
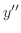 |
 |
![$\displaystyle c_{1}e^{-x} + 9e^{-3x}[c_{2}\cos{2x} + c_{3}\sin{2x}]$](img819.png) |
|
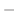 |
![$\displaystyle 6e^{-3x}[-2c_{2}\sin{2x} + 2c_{3}\cos{2x}] + e^{-3x}[-4c_{2}\cos{2x} - 4c_{3}\sin{2x}]$](img821.png) |
| 0 |  |
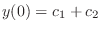 |
(2.1) |
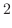 |
 |
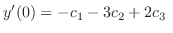 |
(2.2) |
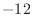 |
 |
 |
(2.3) |
 implies
implies
 .
Therefore,
.
Therefore,
![$\displaystyle y = \frac{4}{3}e^{-x} - e^{-3x}[\frac{4}{3}\cos{2x} + \frac{1}{3}\sin{2x}] \ \ $](img827.png)
(d) Let
 . Then we have the characteristic equation
. Then we have the characteristic equation
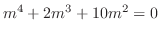 .
.
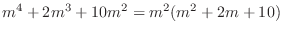
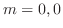 and
and
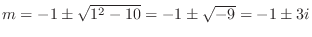 . Thus the fundamental solutions are
. Thus the fundamental solutions are
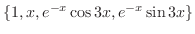
![$\displaystyle y = c_{1} + c_{2}x + e^{-x}[c_{3}\cos{3x} + c_{4}\sin{3x}] $](img833.png)
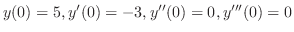 and
and
 |
 |
![$\displaystyle c_{2} - e^{-x}[c_{3}\cos{3x} + c_{4}\sin{3x}]$](img835.png) |
|
 |
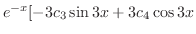 |
||
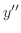 |
 |
![$\displaystyle e^{-x}[c_{3}\cos{3x} + c_{4}\sin{3x}]$](img837.png) |
|
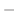 |
![$\displaystyle 2e^{-x}[-3c_{3}\sin{3x} + 3c_{4}\cos{3x}] + e^{-x}[-9c_{3}\cos{3x} - 9c_{4}\sin{3x}]$](img838.png) |
||
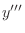 |
 |
![$\displaystyle - e^{-x}[c_{3}\cos{3x} + c_{4}\sin{3x}] + 3e^{-x}[-3c_{3}\sin{3x} + 3c_{4}\cos{3x}]$](img840.png) |
|
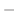 |
![$\displaystyle 3e^{-x}[-9c_{3}\cos{3x} - 9c_{4}\sin{3x}] + e^{-x}[27c_{3}\sin{3x} -27c_{4}\cos{3x}]$](img841.png) |
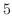 |
 |
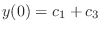 |
(2.4) |
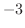 |
 |
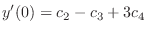 |
(2.5) |
| 0 |  |
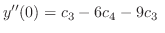 |
(2.6) |
| 0 |  |
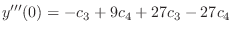 |
(2.7) |
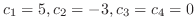 . Thus,
. Thus,