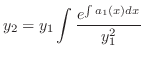Next: Higer Order Homogeneous Linear Up: Linear Differential Equations Previous: Solution of Linear Differential 目次 索引
2. Suppose that one of the solutions of
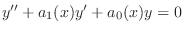 is
is 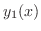 ,then the other solution
,then the other solution 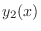 by using the reduction of order is given by
by using the reduction of order is given by
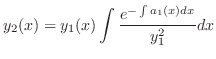
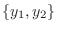 are linearly independent.
are linearly independent.
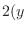 |
 |
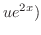 |
|
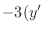 |
 |
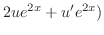 |
|
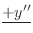 |
 |
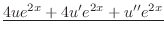 |
|
| 0 |  |
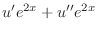 |
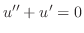
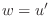 . Then
. Then
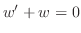
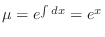 . Multiply
. Multiply  to both sides of equation, we have
to both sides of equation, we have
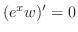 . Solving this, we have
. Solving this, we have
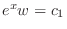 and
and
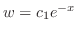
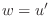 , we have
, we have
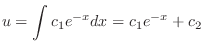
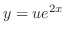 and we obtain the general solution.
and we obtain the general solution.
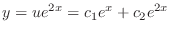
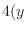 |
 |
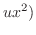 |
|
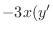 |
 |
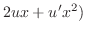 |
|
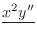 |
 |
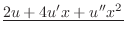 |
|
| 0 |  |
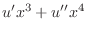 |
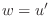 . Then
. Then
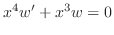
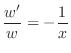
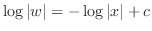 . Thus,
. Thus,
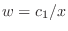 .
Note that
.
Note that
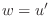 . Then
. Then
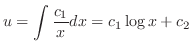
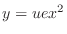 . Then we have the general solution.
. Then we have the general solution.
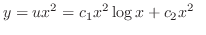
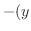 |
 |
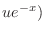 |
|
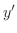 |
 |
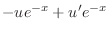 |
|
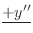 |
 |
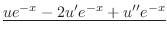 |
|
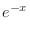 |
 |
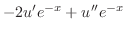 |
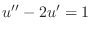
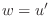 . Then
. Then
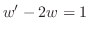
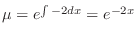 .
Multiply
.
Multiply  to both sides of equation. Then the left-hand side is the derivative of the product of
to both sides of equation. Then the left-hand side is the derivative of the product of  and
and 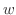 .
.
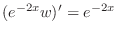
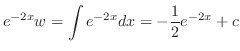
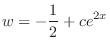
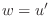 .
.
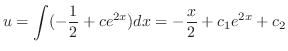
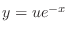 . Then we have the general solution.
. Then we have the general solution.
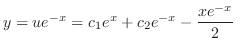
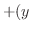 |
 |
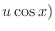 |
|
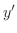 |
 |
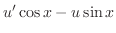 |
|
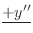 |
 |
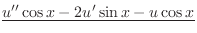 |
|
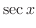 |
 |
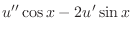 |
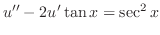
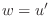 . Then
. Then
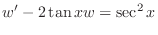
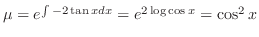 . We multiply
. We multiply  to both sides of equation. Then we get
to both sides of equation. Then we get
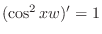 . Solve this equation, we have
. Solve this equation, we have
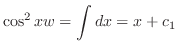
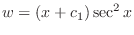
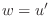 .
.
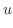 |
 |
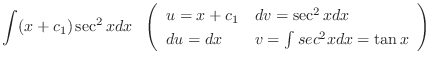 |
|
 |
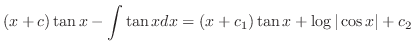 |
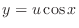 . Then we have the general solution.
. Then we have the general solution.
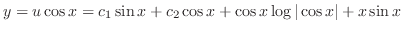
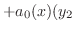 |
 |
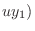 |
|
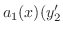 |
 |
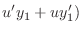 |
|
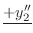 |
 |
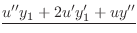 |
|
| 0 |  |
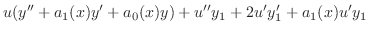 |
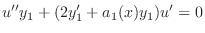
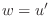 . Then we have
. Then we have
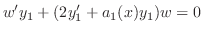
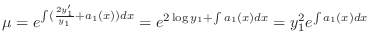
 to both sides. Then the left-hand side is the derivative of the product of
to both sides. Then the left-hand side is the derivative of the product of  and
and 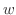 .
.
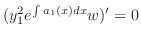
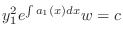
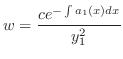
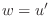 . Then
. Then
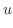 |
 |
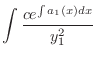 |
|
 |
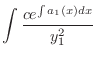 |
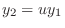 . Then
. Then