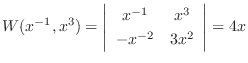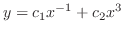Next: Reduction of Order Up: Linear Differential Equations Previous: Linear Differential Equations 目次 索引
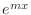 . Find the n independent solutions. Then show the general solution. Also, show that the solutons are linearly independent by using Wronski's determinant.
. Find the n independent solutions. Then show the general solution. Also, show that the solutons are linearly independent by using Wronski's determinant.
(a)
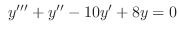
(b)
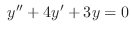
(c)
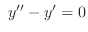
(d)
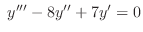
2. The following differential equations have the solution of the form
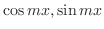 . Find the general solution..
. Find the general solution..
(a)
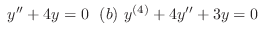
3. The following differential equations have the solution of the form 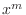 . FInd the general solution.
. FInd the general solution.
(a)
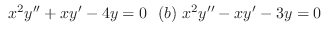
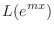 |
 |
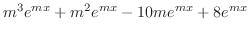 |
|
 |
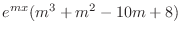 |
||
 |
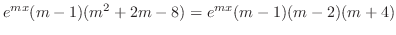 |
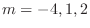 ,
,
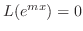 . Thus,
. Thus,
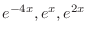 are solutions and
are solutions and
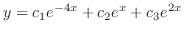
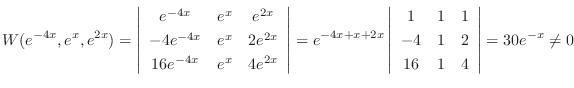
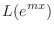 |
 |
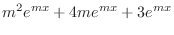 |
|
 |
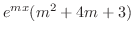 |
||
 |
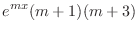 |
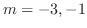 ,
,
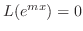 . Thus,
. Thus,
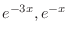 are solutions and the general solution is
are solutions and the general solution is
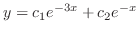
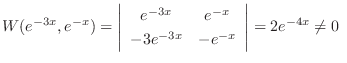
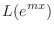 |
 |
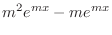 |
|
 |
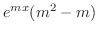 |
||
 |
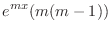 |
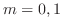 ,
,
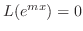 . Then
. Then 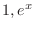 are solutions and the general solution is
are solutions and the general solution is
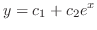
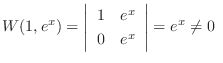
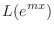 |
 |
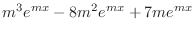 |
|
 |
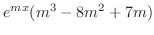 |
||
 |
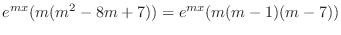 |
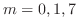 ,
,
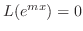 . Then
. Then
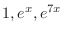 are solutions and the general solution is
are solutions and the general solution is
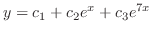
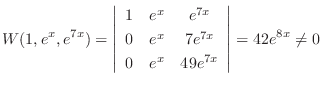
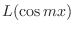 |
 |
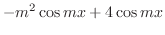 |
|
 |
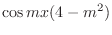 |
||
 |
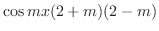 |
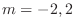 ,
,
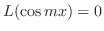 . Thus,
. Thus,
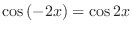 is a solution.
is a solution.
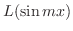 |
 |
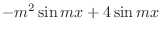 |
|
 |
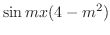 |
||
 |
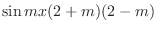 |
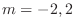 ,
,
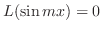 . Thusm
. Thusm
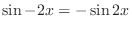 is also a solution. Note that for
is also a solution. Note that for 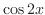 and
and 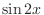 , we have
, we have
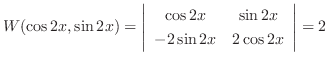
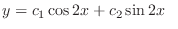
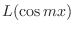 |
 |
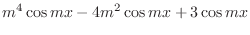 |
|
 |
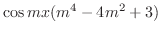 |
||
 |
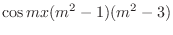 |
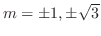 ,
,
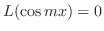 . Then
. Then
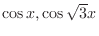 are solutions.
are solutions.
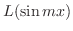 |
 |
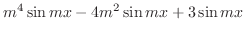 |
|
 |
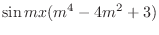 |
||
 |
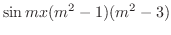 |
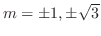 ,
,
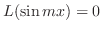 . Thus,
. Thus,
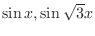 are also solutions. Now we check to see
are also solutions. Now we check to see
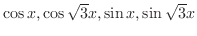 are linearly independent.
are linearly independent.
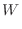 |
 |
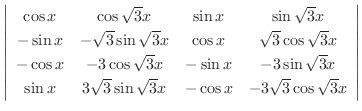 |
|
 |
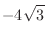 |
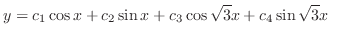
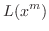 |
 |
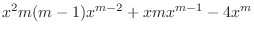 |
|
 |
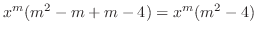 |
||
 |
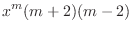 |
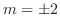 ,
,
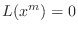 . Thus,
. Thus,
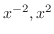 are solutions.
Note that
are solutions.
Note that
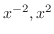 satisfies
satisfies
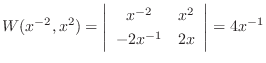
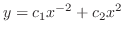
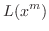 |
 |
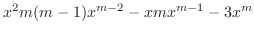 |
|
 |
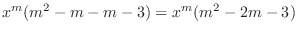 |
||
 |
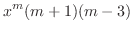 |
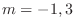 ,
,
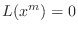 . Thus,
. Thus,
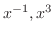 are solutions.
Note that
are solutions.
Note that
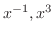 satisfies
satisfies