Next: Variation of Parameter Up: Linear Differential Equations Previous: Higer Order Homogeneous Linear 目次 索引
Answer
1.
(a) Given auxiliary equation
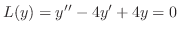 , we have the characterisitc equation
, we have the characterisitc equation
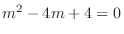 . Then characteristic roots are
. Then characteristic roots are 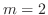 double roots. Then the complementary solution
double roots. Then the complementary solution 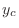 is
is
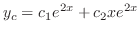
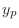 using the method of undetermined coefficients. Let
using the method of undetermined coefficients. Let
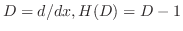 . Then
. Then
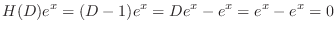
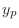 is a solution of
is a solution of
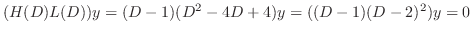
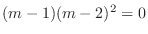 . Then the characteristic roots are
. Then the characteristic roots are
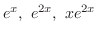 . But
. But
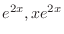 are solutions of the complementary function. So, we can not use them. So, we write
are solutions of the complementary function. So, we can not use them. So, we write
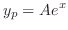
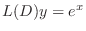 . Then
. Then
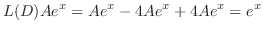
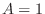 . Thus, the particular solution is
. Thus, the particular solution is
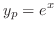
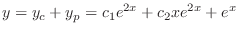
(b) Given the auxiliary equation
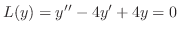 , we have the characteristic equation
, we have the characteristic equation
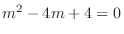 . Then the characteristic roots are
. Then the characteristic roots are
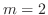 double roots. Thus the complementary function
double roots. Thus the complementary function 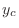 is
is
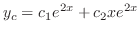
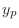 using the method of undetermined coefficients. Let
using the method of undetermined coefficients. Let
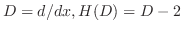 . Then
. Then
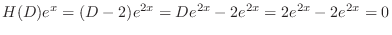
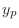 is a solution of the following
is a solution of the following
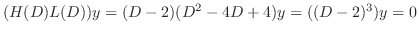
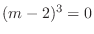 . Then the fundamental solutions are
. Then the fundamental solutions are
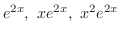 . But
. But
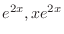 are the solutions of the complementary function. Thus we omit those solutions. Then we have
are the solutions of the complementary function. Thus we omit those solutions. Then we have
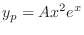
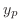 to the equation
to the equation
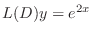 . Then
. Then
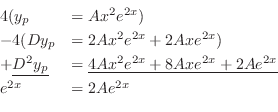
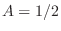 . Therefore the particular solution is
. Therefore the particular solution is
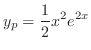
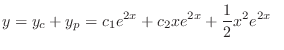
(c) Given the auxiliary equation
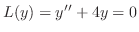 . We have the characteristic equation
. We have the characteristic equation
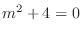 . Then the characteristic roots are
. Then the characteristic roots are
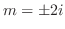 . Thus the complementary function
. Thus the complementary function 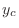 is
is
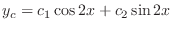
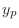 using the method of undetermined coefficients. Let
using the method of undetermined coefficients. Let
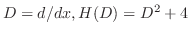 . Then
. Then
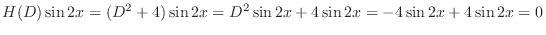
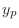 is a solution of the following
is a solution of the following
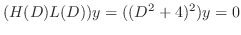
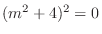 . Then the fundamental solutions are
. Then the fundamental solutions are
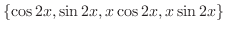
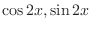 are solutions of the complementary function. Thus we omit those solutions. Then we have
are solutions of the complementary function. Thus we omit those solutions. Then we have
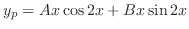
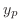 to
to
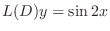 . Then
. Then
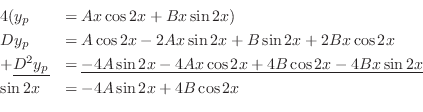
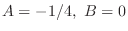 . Then
. Then
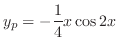
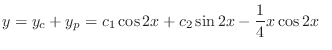
(d) Given the auxiliary equation
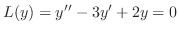 . We have the characteristic equation
. We have the characteristic equation
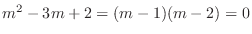 . Then the characteristic roots are
. Then the characteristic roots are
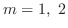 . Thus the complementary function
. Thus the complementary function 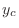 is
is
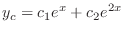
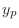 using the method of undetermined coefficients. By superposition principal, if we find the particular solution
using the method of undetermined coefficients. By superposition principal, if we find the particular solution 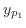 of
of
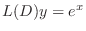 ,
,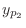 of
of
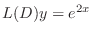 ,
, 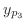 of
of
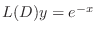 , then
, then
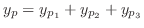 .
.
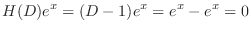
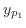 is a solution of the following
is a solution of the following
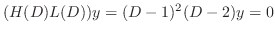
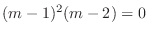 . Then the fundamental solutions are
. Then the fundamental solutions are
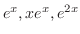 . But
. But
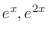 are solutions of the complementary function. So we omit those solutions. Then
are solutions of the complementary function. So we omit those solutions. Then
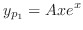
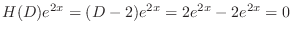
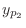 is a solution of the following
is a solution of the following
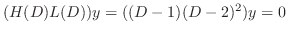
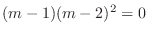 . Then the fundamental solutions are
. Then the fundamental solutions are
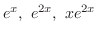 . but
. but
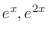 are solutions of the complementary function. So we omit those solutions. Then
are solutions of the complementary function. So we omit those solutions. Then
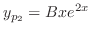
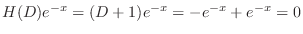
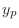 is a solution of the following
is a solution of the following
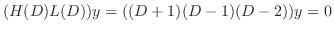
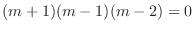 . Then the fundamental solutions are
. Then the fundamental solutions are
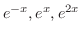 . But
. But
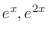 are solutions of the complementary function. So we omit those solutions. Then
are solutions of the complementary function. So we omit those solutions. Then
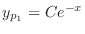
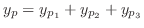 to
to
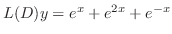 . Then
. Then
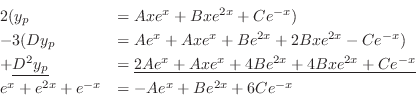
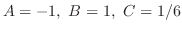 . Thus, the particular solution is
. Thus, the particular solution is
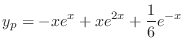
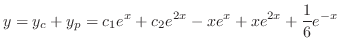
(e) Given the auxiliary equation
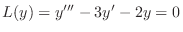 . We have the characteristic equation
. We have the characteristic equation
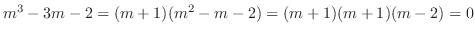 . Then the characteristic roots are
. Then the characteristic roots are
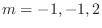 . Thus the complementary function
. Thus the complementary function 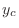 is
is
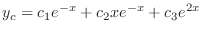
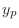 using the method of undermined coefficient. Let
using the method of undermined coefficient. Let
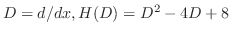 . Then
. Then
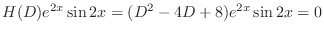
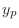 is a soluton of the following equation.
is a soluton of the following equation.
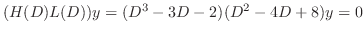
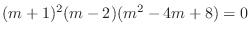 . Then the fundamental solutions are
. Then the fundamental solutions are
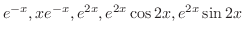 . But
. But
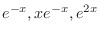 are solutions of the complementary function. Thus we omit those solutions. Then
are solutions of the complementary function. Thus we omit those solutions. Then
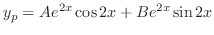
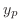 into
into
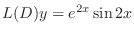 . Then
. Then
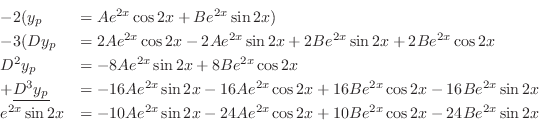
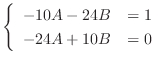
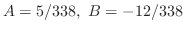 . Thus, the particular solution is
. Thus, the particular solution is
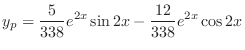
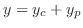 |
 |
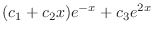 |
|
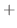 |
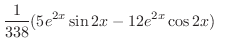 |
(f) Given auxiliary equation
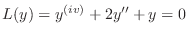 . Then the characteristic equation is
. Then the characteristic equation is
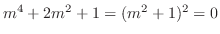 . Thus, the characteristic roots are
. Thus, the characteristic roots are
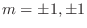 . Thus the complementary function
. Thus the complementary function  is
is
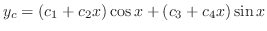
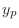 using the method of undetermined coefficient. Let
using the method of undetermined coefficient. Let
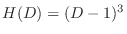 . Then
. Then
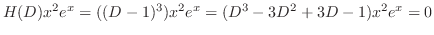
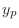 is a solution of the following equation.
is a solution of the following equation.
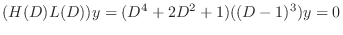
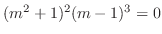 . Thus the fundamental solutions are
. Thus the fundamental solutions are
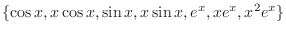
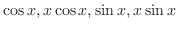 are solutions of the complementary function. Thus we omit those solutions. Then we have
are solutions of the complementary function. Thus we omit those solutions. Then we have
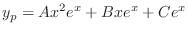
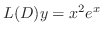 . Then
. Then
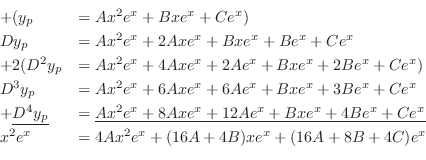
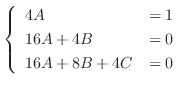
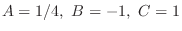 . Thus, the particular solution is
. Thus, the particular solution is
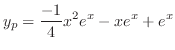
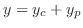 |
 |
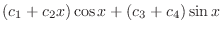 |
|
 |
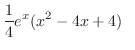 |