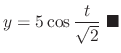Next: Exercise Up: Linear Differential Equations Previous: Exercise Contents Index
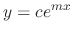 is a complete solution of
is a complete solution of
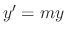 . Then we use
. Then we use
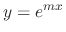 as a candidate for the solution of the following
as a candidate for the solution of the following 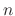 th-order linear differential equation.
th-order linear differential equation.
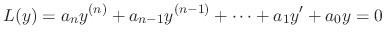
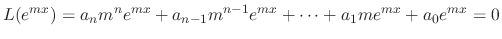
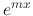 is a solution of
is a solution of 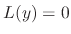 if and only if
if and only if
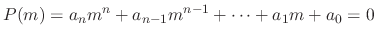
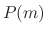 is called the characteristic polynomial, and
is called the characteristic polynomial, and 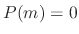 is called the characteristic equation. This way, we only need to solve the polynomial equation
is called the characteristic equation. This way, we only need to solve the polynomial equation 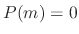 instead of solving
instead of solving 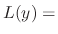 .
.
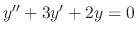 .
.
SOLUTION
The roots of the characteristic equation
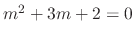 are
are
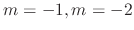 . Then
. Then 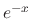 and
and 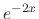 are solutions and by example 2.2, these solutions are linearly independent. Thus, the general solution is
are solutions and by example 2.2, these solutions are linearly independent. Thus, the general solution is
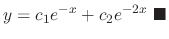
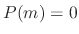 of the
of the 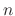 th -order linear differential equation are distinct real roots
th -order linear differential equation are distinct real roots
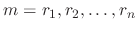 . Then the set of solutions
. Then the set of solutions
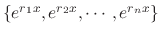 is a basis for the solution space.
is a basis for the solution space.
Proof.
We show
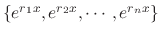 are linearly independent by using Wronskian. Then
are linearly independent by using Wronskian. Then
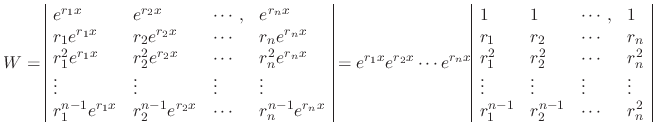
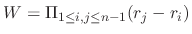 . Since
. Since 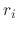 are distinct real roots,
are distinct real roots, 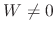 .
.
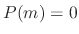 of the 4th-order homogeneous linear differential equation
of the 4th-order homogeneous linear differential equation 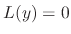 are
are
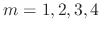 . Then find the general solution.
. Then find the general solution.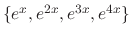 is the basis of the solution space. Thus, the general solution is the linear combination of
is the basis of the solution space. Thus, the general solution is the linear combination of
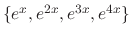 . Therefore,
. Therefore,
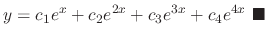
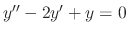 .
.
SOLUTION
The roots of the characteristic equation
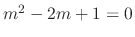 are
are 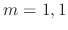 . Then
. Then
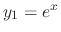 is a solution.
Since this differential equation is the 2nd-order, we must have another linearly independent solution. By exercise 2.2.1,
is a solution.
Since this differential equation is the 2nd-order, we must have another linearly independent solution. By exercise 2.2.1, 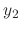 can be obtained by
can be obtained by
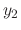 |
 |
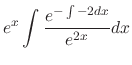 |
|
 |
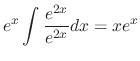 |
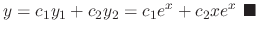
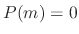 are
are 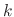 -fold multiple roots
-fold multiple roots 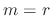 . Then
. Then
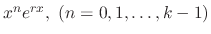 are the solutions of the differential equation
are the solutions of the differential equation 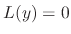 . Furthermore, the set of solutions
. Furthermore, the set of solutions
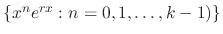 is a basis of the solution space.
is a basis of the solution space.
Proof
Denote
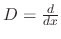 . Then we can express
. Then we can express
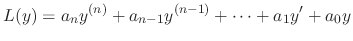
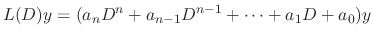
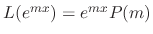 , we have
, we have
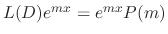 . Now evaluate
. Now evaluate
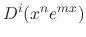 . Then
. Then
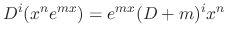
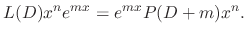
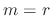 is
is 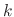 -fold multiple roots,
-fold multiple roots,
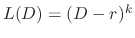 and
and
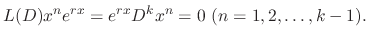
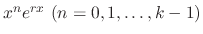 are linearly independent.
are linearly independent.
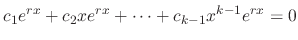
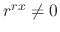 , we have
, we have
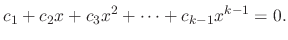
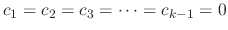 .
.

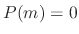 of the 4th-order linear differential equation
of the 4th-order linear differential equation 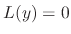 are
are
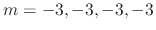 , then find the general solution.
, then find the general solution.
SOLUTION
By the theorem 2.9,
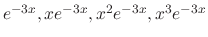 are linearly independent solutions of
are linearly independent solutions of 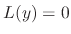 . Thus the general solution is
. Thus the general solution is
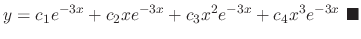
Let the coefficients of 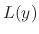 be real. If
be real. If 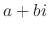 is the root of the characteristic equation
is the root of the characteristic equation 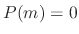 , then the conjugate
, then the conjugate 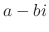 is also a root.
Thus,
is also a root.
Thus,
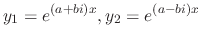
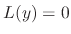 .
Now by the Euler's formula,
.
Now by the Euler's formula,
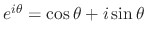 , and the linearlity of solutions
, and the linearlity of solutions
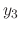 |
 |
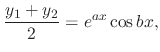 |
|
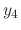 |
 |
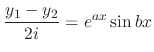 |
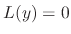 . It is not hard to show
. It is not hard to show 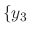 and
and 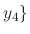 are linearly independent. Thus, the basis of the solutions corresponding to
are linearly independent. Thus, the basis of the solutions corresponding to 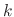 -fold multiple roots of complex numbers is
-fold multiple roots of complex numbers is
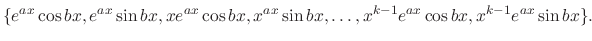
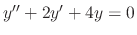 .
.
SOLUTION
The roots of the characteristic equation
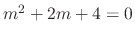 are
are
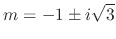 . Then
. Then
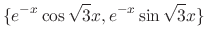
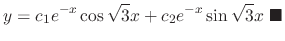
The mass of the object is  , the spring constant is
, the spring constant is  , The force loss due to friction of dashpot is proportional to the speed of the object
, The force loss due to friction of dashpot is proportional to the speed of the object 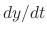 . Then the forces acting on the object is given by
. Then the forces acting on the object is given by
1. 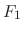 |
= 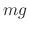 the gravitational force the gravitational force |
2. 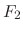 |
= 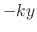 the restoring force by the spring the restoring force by the spring |
3. 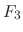 |
=
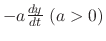 force due to friction force due to friction |
4. 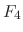 |
= 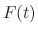 the external force the external force
|
Now using the Newton's 2nd law, we have
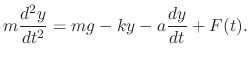
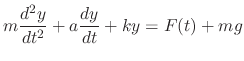
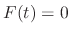 ,
, 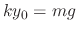 . Then for
. Then for 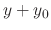 , we have
, we have
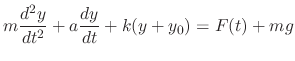
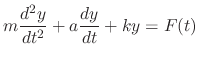
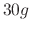 to its lower end, it stretched
to its lower end, it stretched 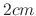 . From this position you have stretched the spring
. From this position you have stretched the spring 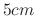 and release. Find the motion of the spring.
and release. Find the motion of the spring.
SOLUTION
By Hooke's law, we have the spring constant
 . Then by the Newton's 2nd law, we have
. Then by the Newton's 2nd law, we have
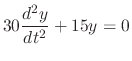
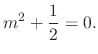
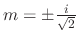 . Thus,
. Thus,
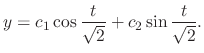
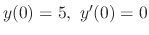 , we have
, we have