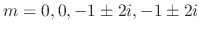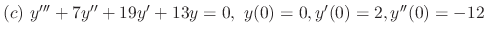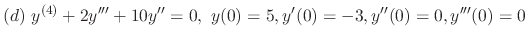Exercise

1. Find the fundamental solutions of the following differential equations.
$$\begin{array}{ll} (a) \ y^{\prime\prime} + 9y = 0 & (b) \ y^{... ...^{(5)} + 18y{\prime\prime\prime} + 81y^{\prime} = 0 \end{array}$$
2. Find the general solutions.
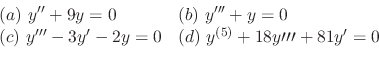
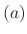$(a)$ The roots of the characteristic equation of the 4th-order linear homogeneous differential equation are $m = -2,1,1,1$
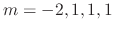
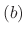$(b)$ The roots of the characteristic equation of the 6th-order linear homogeneous differential equation are $m = 0,0,-1\pm2i,-1\pm2i$
3. Solve the following initial value problems.
$(a) \ y^{\prime\prime} - y = 0, \ y(0) = 1, y^{\prime}(0) = 1$
$(b) \ y^{\prime\prime} -6y^{\prime} +9y = 0, \ y(0) = 1, y^{\prime}(0) = 2$
$(c) \ y^{\prime\prime\prime} + 7y^{\prime\prime} + 19y^{\prime} + 13y = 0, \ y(0) = 0, y^{\prime}(0) = 2, y^{\prime\prime}(0) = -12$
$(d) \ y^{(4)} + 2y^{\prime\prime\prime} + 10y^{\prime\prime} = 0, \ y(0) = 5, y^{\prime}(0) = -3, y^{\prime\prime}(0) = 0, y^{\prime\prime\prime}(0) = 0$