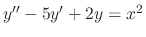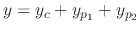Next: Exercise Up: Linear Differential Equations Previous: Linear Differential Equations Contents Index
The differential equation of the form
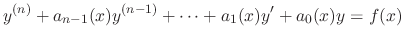
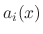 is called the coefficient function.
is called the coefficient function.
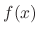 is called the input function.
is called the input function.
If
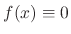 , then the differntial equation is called the homogeneous equation.
, then the differntial equation is called the homogeneous equation.
We denote the left-hand side as 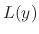 . Then the differential equation is expressed as
. Then the differential equation is expressed as
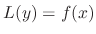
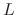 is called the differential operator and has linearlity. That is for any solutions
is called the differential operator and has linearlity. That is for any solutions
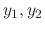 and constants
and constants
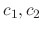 ,
,
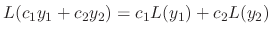
We review the vector space.
A sum of two vectors A and B is expressed as A 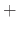 B and is equal to the diagonal of the parallelogram formed by A and B.
B and is equal to the diagonal of the parallelogram formed by A and B.
1. A sum of two vetors is a vector (closure)
2. For any vectors A and B,A+B = B+A (commutative law)
3. For any vectors A,B,C, (A+B)+C = A+(B+C) (associative law)
4. Given any vector A, there exists a vector 0 satisying A+0 = A (existence of zero)
5. Given any vector A, there exists a vector B satisfying A+B = 0 (existence of inverse)
6. A scalar multiplication of a vector is a vector
7. For any real numbers 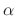 and
and 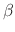 ,
, 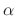 (
(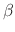 A) = (
A) = (
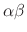 )A (associative law)
)A (associative law)
8. For any real numbers 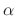 and
and 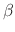 , (
, (
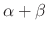 )A =
)A = 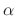 A +
A + 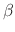 A and for any vectors A and B,
A and for any vectors A and B, 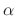 (A+B) =
(A+B) = 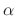 A +
A + 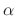 B (distributive law)
B (distributive law)
9. 1A = A; 0A = 0; 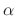 0 = 0 (1 is multiplicative identity)
0 = 0 (1 is multiplicative identity)
Let 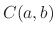 be the set of continuous functions on the interval
be the set of continuous functions on the interval 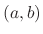 . Let
. Let 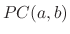 be the set of piecewise continuous functions on
be the set of piecewise continuous functions on 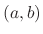 , 2.1
, 2.1
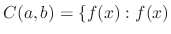 is continuous on
is continuous on 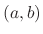 },
},
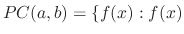 is piecewise continuous on
is piecewise continuous on 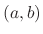 }.
}.
For 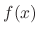 and
and 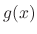 in
in 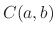 or
or 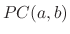 , we define the addition on the scalar multiplication as follows:
, we define the addition on the scalar multiplication as follows:
1. 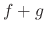 is a function of
is a function of  whose value is equal to
whose value is equal to 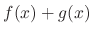 .
.
2. 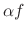 is a function of
is a function of  whose value is equal to
whose value is equal to
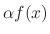 .
.
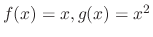 , find
, find
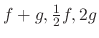 .
.
SOLUTION
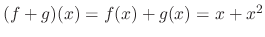
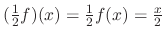
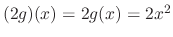

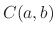 with the operation defined above is a vector space. Then the function
with the operation defined above is a vector space. Then the function 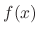 belongs to
belongs to 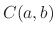 is called a vector.
is called a vector.
Proof
The solutions of a homogeneous differential equation are differentiable. Thus, the set of solutions are the subset of continuous functions. Then to show 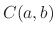 is a vector space, it is enough to show the linear combination of the solutions
is a vector space, it is enough to show the linear combination of the solutions 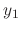 and
and 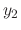 is a solution.
Let
is a solution.
Let
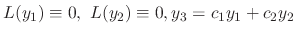 . Then
. Then
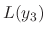 |
 |
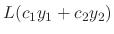 |
|
 |
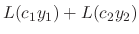 |
||
 |
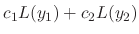 |
||
 |
0 |
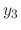 is again a solution.
is again a solution.

The set of solutions of homogeneous equation becomes a vector space. So, we call this solution space.
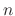 independent solutions of homogeneous differential equation.
independent solutions of homogeneous differential equation.
The determinant of the following matrix is called Wronskian determinant. Let 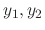 be the solutions of the differential equation. Then
be the solutions of the differential equation. Then
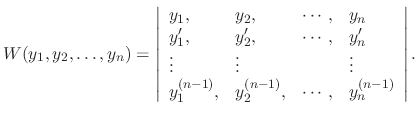
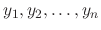 are the solutions of the homogeneous equation on the interval
are the solutions of the homogeneous equation on the interval ![$[a,b]$](img46.png) , then
, then
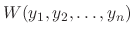 is either 0 or never 0 0n the interval
is either 0 or never 0 0n the interval ![$[a,b]$](img46.png) .
.
Proof
For 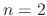 Since
Since 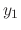 and
and 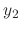 are solutions of
are solutions of
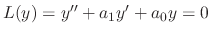 , we have
, we have
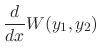 |
 |
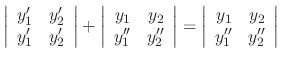 |
|
 |
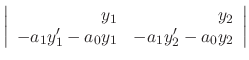 |
||
 |
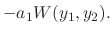 |
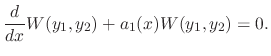
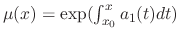 . Multiplying
. Multiplying 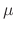 to get
to get
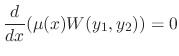
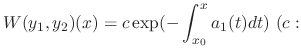 constant
constant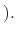
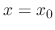 . Then
. Then
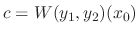 and
and
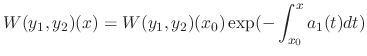

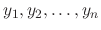 are solutions of the homogeneous differential equation on
are solutions of the homogeneous differential equation on ![$[a,b]$](img46.png) , then the following conditions are equivalent.
, then the following conditions are equivalent.
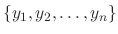 are linearly independent on the interval
are linearly independent on the interval ![$[a,b]$](img46.png) .
.
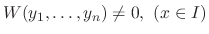
Proof
For 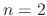 , let the linear combination of
, let the linear combination of 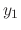 and
and 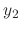 be 0. Then
be 0. Then
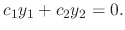
 . Then
. Then
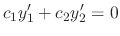
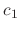 and
and 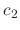 .
.
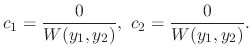
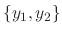 are linearly independent, then
are linearly independent, then
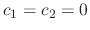 . Thus,
. Thus,
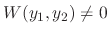 . Conversely, if
. Conversely, if
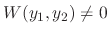 , then
, then
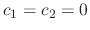 . Thus,
. Thus,
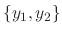 are linearly independent
are linearly independent

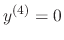 .
.
SOLUTION
The dimension of the solution space is 3.
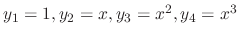 are solutions of the differential equation. So, we need to show they are linearly independent.
are solutions of the differential equation. So, we need to show they are linearly independent.
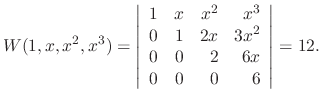
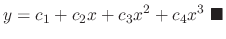
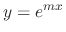 is a solution of
is a solution of
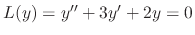 . Then find the fundamental solution.
. Then find the fundamental solution.
SOLUTION
Since
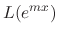 |
 |
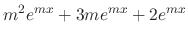 |
|
 |
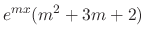 |
||
 |
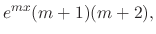 |
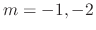 implies that
implies that
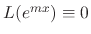 .
.
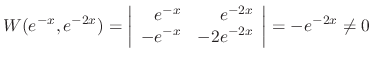
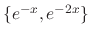 are fundamental solutions.
are fundamental solutions.

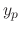 is an particular solution of
is an particular solution of  the-order linear differential equation
the-order linear differential equation
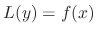 and
and 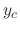 is the general solution of
is the general solution of 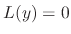 . Then
. Then
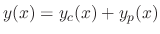 is the general solution of
is the general solution of
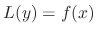 .
.
Proof
By the assumption,
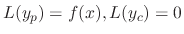 . Now by the linearlity of
. Now by the linearlity of 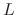 , we have
, we have
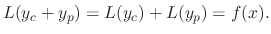
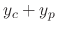 is a solution of
is a solution of
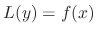 . Since
. Since 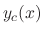 contains
contains 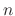 constants,
constants,
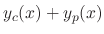 is the general solution.
is the general solution.

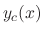 is called the complementary solution. By this theorem, if an particular solution of
is called the complementary solution. By this theorem, if an particular solution of
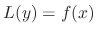 is found, then to find the general solution, it is enough to find a complementary solution of
is found, then to find the general solution, it is enough to find a complementary solution of 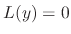 .
.
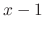 is an particular solution of
is an particular solution of
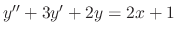 . Then find the general solution.
. Then find the general solution.
SOLUTION
Since
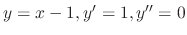 ,
,
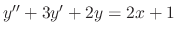 . Also, the complementary solution of
. Also, the complementary solution of 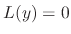 is given in example2.2. Thus
is given in example2.2. Thus
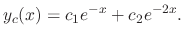
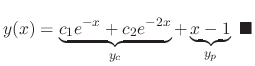
If 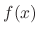 is given as a sum of
is given as a sum of 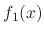 and
and 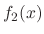 , then it is better to consider
, then it is better to consider
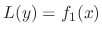 and
and
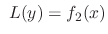 .
.
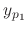 is a solution of
is a solution of
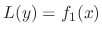 , and
, and 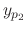 is a solution of
is a solution of
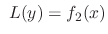 . Then
. Then
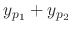 is a solution of
is a solution of
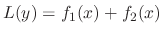 .
.Proof.
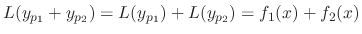
For example, to find the general solution of the differential equation
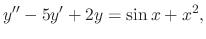
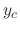 of
of
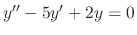
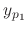 of
of
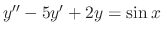
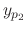 of
of