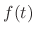 is said to be piecewise continuous on the interval
is said to be piecewise continuous on the interval ![$[a,b]$](img46.png) if the function satisies the following conditions:
(i)
if the function satisies the following conditions:
(i) 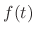 is continuous on the intervval
is continuous on the intervval ![$[a,b]$](img46.png) except at finite number of points.
except at finite number of points.
(ii) The left-hand limit and the right-hand limit exist at discontinuous point
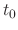 of
of 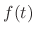 .
.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .