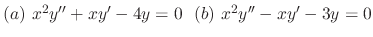Next: Reduction of order Up: Solution of linear differential Previous: Solution of linear differential Contents Index
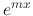 . Find the
. Find the 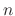 independent solutions and the general solution. Finally,show the
independent solutions and the general solution. Finally,show the 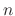 solutions are linearly independent.
solutions are linearly independent.
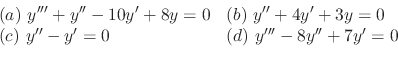
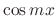 or
or 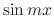 . Find the general solution.
. Find the general solution.
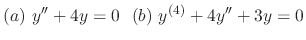
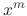 . Find the general solution.
. Find the general solution.