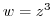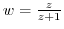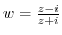Next: Linear function Up: Complex functions Previous: Complex functions Index
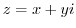 in one region
in one region  on the complex plane, one complex number
on the complex plane, one complex number
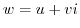 ,
,
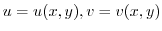 corresponds,
corresponds,  is called a complex function defined in the region
is called a complex function defined in the region  , and
, and
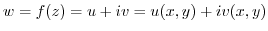 . This region
. This region  is called the domain of
is called the domain of  .
.
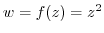 is all plane and
is all plane and
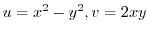
The domain of
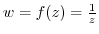 is all plane except the origin and
is all plane except the origin and
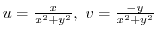
Since the complex function 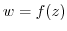 is considered to be a mapping of the point
is considered to be a mapping of the point  on the
on the  plane to the point
plane to the point 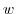 on the
on the 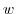 plane, the mapping
plane, the mapping 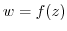 At this time,
At this time, 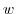 is called an image and
is called an image and  is called an original image.
is called an original image.
In general, the value of 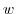 corresponding to one
corresponding to one  is not limited to one, but in my lecture, unless otherwise specified, only one value of
is not limited to one, but in my lecture, unless otherwise specified, only one value of 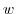 corresponds to a monovalent function.
corresponds to a monovalent function.
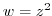 , express
, express 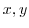 using
using 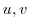 function and find out what curve is mapped to the
function and find out what curve is mapped to the 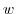 plane parallel to the real and imaginary axes of the
plane parallel to the real and imaginary axes of the  plane.
plane.
2. Express 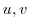 as a function of
as a function of 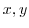 for the following function
for the following function