Next: Linear function Up: Solution Previous: 1.2 DeMoivre's theorem and Index
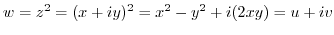
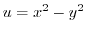 ,
, 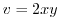 . Next we solve this for
. Next we solve this for  .
.
Since 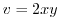 ,
,
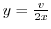 . Put this into
. Put this into
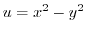 . Then
. Then
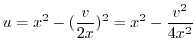
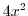 . Then
. Then
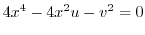
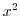 . Thus let
. Thus let 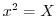 . Then.
by the formula of quadratic equation, we have
. Then.
by the formula of quadratic equation, we have
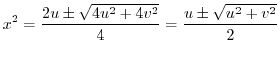
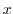 is a real part. Thne
is a real part. Thne
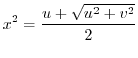
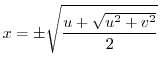
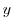 . Since
. Since
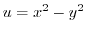 , we have
, we have
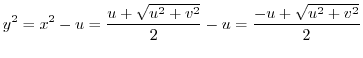
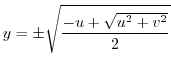
Next, consider what kind of curve the straight line
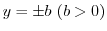 parallel to the real axis of the
parallel to the real axis of the  plane is mapped.
By the above equation,
plane is mapped.
By the above equation, 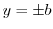 satisfies
satisfies
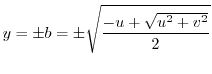
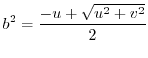
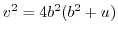
Similarly, a straight line parallel to the imaginary axis of the  plane
plane
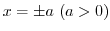 satifies
satifies
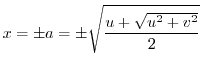
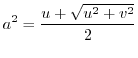
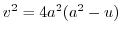 .
.
2.
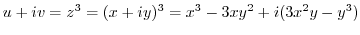
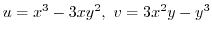 .
.
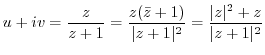
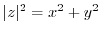 .
.
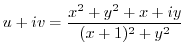
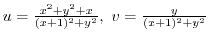 .
.
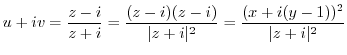
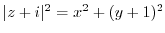 . Then
. Then
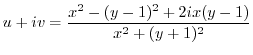
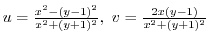 .
.