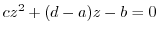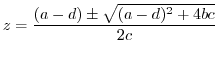Next: 2.3 Elementary functions Up: Solution Previous: 2.1 Complex function Index
1.
(a)
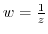 takes
takes 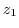 by inverting the point
by inverting the point  with respect to the unit circle
with respect to the unit circle 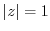 , and then takes symmetrical transformation of
, and then takes symmetrical transformation of 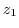 .
.
Since the two points P and Q are on the unit circle, they appear at points P'and Q'symmetrical with respect to the real axis by
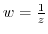 . Also, the point at infinity of a straight line is reflected at the origin. Furthermore,
. Also, the point at infinity of a straight line is reflected at the origin. Furthermore,
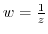 is circle to circle, this straight line maps to the circle going through P', Q'.
is circle to circle, this straight line maps to the circle going through P', Q'.
(b)
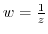 takes
takes 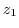 by inverting the point
by inverting the point  with respect to the unit circle
with respect to the unit circle 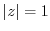 , and then takes symmetrical transformation of
, and then takes symmetrical transformation of 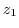 .
.
Since the point P is on the unit circle, it maps to the point P' which is symmetric with respect to the real axis by
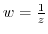 . Also, the point at infinity of a straight line is reflected at the origin. Furthermore,
. Also, the point at infinity of a straight line is reflected at the origin. Furthermore,
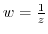 is circle to circle. This straight line maps to the circle with the radius of the distance from the orign to P'.
is circle to circle. This straight line maps to the circle with the radius of the distance from the orign to P'.
(c)
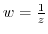 takes
takes 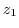 by inverting the point
by inverting the point  with respect to the unit circle
with respect to the unit circle 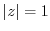 , and then takes symmetrical transformation of
, and then takes symmetrical transformation of 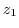 .
.
A point 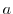 maps to
maps to
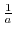 , a point
, a point 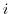 maps to
maps to
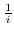 , a point
, a point 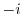 maps to
maps to
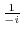 . Furthermore,
. Furthermore,
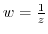 is circle to circle, a cricle going through 3 points
is circle to circle, a cricle going through 3 points 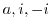 maps to a circle going through 3 points
maps to a circle going through 3 points
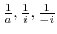 .
.
2.
(a) An invariant point is a point that satisfies 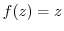 .
.
Let
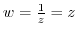 . Then
. Then 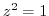 . Thus we use the quadratic formula.
. Thus we use the quadratic formula.
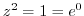 implies the roots are
implies the roots are
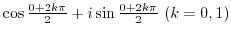 . In other words,
. In other words, 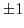 .
.
(b) An invariant point is a point that satisfies 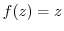 .
.
Let
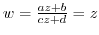 . Then
. Then
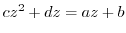 . Rewrite this, we have
. Rewrite this, we have