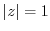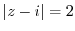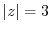Next: Application to real integration Up: Expansion and residue Previous: Laurent's expansion Index
In the Laurent expansion of  centered on the point
centered on the point 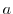 , the series part is set to
, the series part is set to 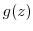 . Then we can write
. Then we can write
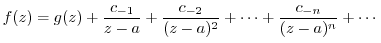
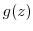 is regular when
is regular when  is centered on a circle of
is centered on a circle of 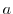 ,
,
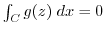 . On the other hand, the series of the principal part converges on
. On the other hand, the series of the principal part converges on  . Therefore, if the Laurent expansion of
. Therefore, if the Laurent expansion of  is term-wise integrated along
is term-wise integrated along  , then we have
, then we have
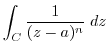 |
 |
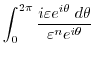 |
|
 |
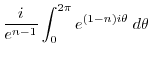 |
||
 |
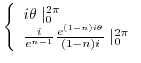 |
||
 |
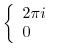 |
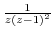
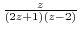
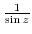
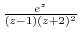
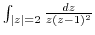
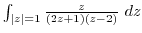
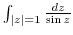
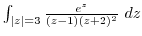
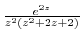 along the following curves.
along the following curves.