Next: Residue Up: Expansion and residue Previous: Expansion and residue Index
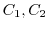 , their radii are
, their radii are
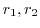 , and
, and 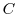 is any concentric circle between
is any concentric circle between 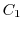 and
and 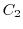 . The function
. The function 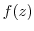 is a circular region surrounded by
is a circular region surrounded by 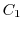 and
and 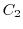 with
with
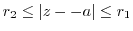 . When monovalent and analytic, for any
. When monovalent and analytic, for any 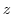 satisfying
satisfying
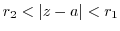 ,
,
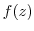 |
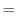 |
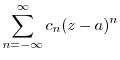 |
|
 |
 |
||
 |
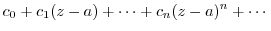 |
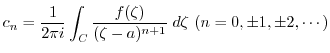
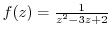 , find the Laurent's expansion centered at the origin for the points in each of the following regions.
, find the Laurent's expansion centered at the origin for the points in each of the following regions.
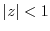
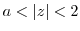
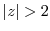
![$\frac{1}{z^{3}(z+1)} [z=0]$](img383.png)
![$\frac{z^3}{(z+1)} [z = -1]$](img384.png)
![$\frac{e^{z^2}}{z^3} [z = 0]$](img385.png)
![$\frac{\sin{z}}{z - \pi} [z = \pi]$](img386.png)