Next: 5.3 Application of real Up: Solution Previous: 5.1 Laurent expansion Index
1. A singular point is a point where the function  is not regular. It is the point where the denominator is 0 in a rational function.
is not regular. It is the point where the denominator is 0 in a rational function.
Basic formula
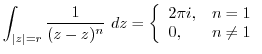
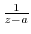 does not become 0 when Laurent expanded, but everything else becomes 0. From this, the coefficient of
does not become 0 when Laurent expanded, but everything else becomes 0. From this, the coefficient of
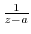 is called a residue, which means that it does not become 0 when integrated, and is expressed as
is called a residue, which means that it does not become 0 when integrated, and is expressed as ![$Res[a]$](img1053.png) .
.
Residue formula For 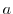 is the singularity of
is the singularity of  with pole of order
with pole of order 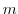 ,
,
![$\displaystyle Res[a] = \frac{1}{(m-1)!}\lim_{z \to a}\frac{d^{m-1}}{dz^{m-1}}(z -a)^{m}f(z)$](img1054.png)
(a) The points where the denominator is 0 are 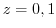 . Then we find the residue of
. Then we find the residue of 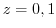 . Expand
. Expand
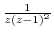 using partial fraction expansion. Then
using partial fraction expansion. Then
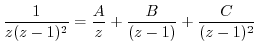
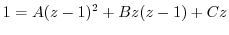
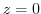 . Then
. Then
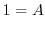
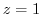 . Then
. Then
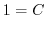
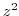 . Then
. Then
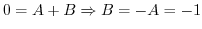
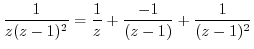
![$\displaystyle Res[0] =$](img1064.png) coefficient of
coefficient of 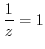
![$\displaystyle Res[1] =$](img1066.png) coefficient of
coefficient of 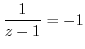
(b) The points where the denominator is 0 are
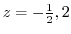 . Then we find the residue of
. Then we find the residue of
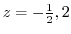 . Expand
. Expand
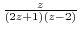 using partial fraction expansion.
using partial fraction expansion.
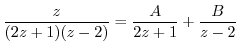
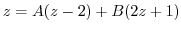
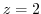 . Then we have
. Then we have
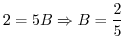
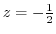 . Then we have
. Then we have
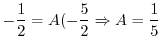
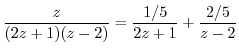
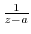 . So, we rewrite
. So, we rewrite
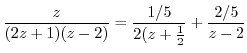
![$\displaystyle Res[2] =$](img1076.png) coefficient of
coefficient of 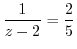
![$\displaystyle Res[-\frac{1}{2}] =$](img1078.png) coefficient of
coefficient of 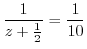
(c) The points where the denominator is 0 are
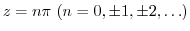 . Then find the residue of
. Then find the residue of 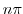 . We can not use the partial fraction expansion on
. We can not use the partial fraction expansion on
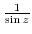 . So, we use Taylor expansion on
. So, we use Taylor expansion on 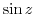 at
at 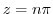 . Then divide. Let
. Then divide. Let
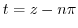 . Then
. Then
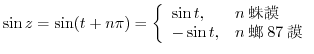
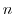 is even.
is even.
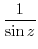 |
 |
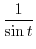 |
|
 |
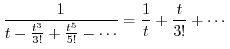 |
||
 |
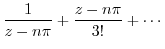 |
![$\displaystyle Res[n\pi] =$](img1089.png) coefficient of
coefficient of 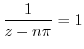
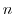 is odd.
is odd.
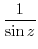 |
 |
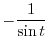 |
|
 |
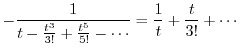 |
||
 |
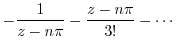 |
![$\displaystyle Res[n\pi] =$](img1089.png) coefficient of
coefficient of 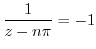
(d) The points where the denominator is 0 are 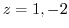 . Then find the residue of
. Then find the residue of 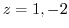 . Expand
. Expand
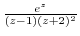 using the partial fraction expansion. Then
using the partial fraction expansion. Then
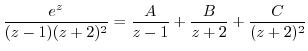
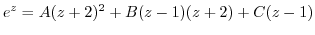
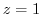 . Then
. Then
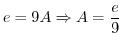
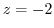 . Then
. Then
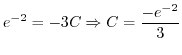
![$\displaystyle Res[1] =$](img1066.png) coefficient of
coefficient of 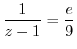
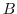 . But we can not use the matching of coefficients. Because,
. But we can not use the matching of coefficients. Because, 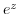 is not polynomial. Then we use Heaviside's expansion theorem or residue formula. Here, we use residue formula.
is not polynomial. Then we use Heaviside's expansion theorem or residue formula. Here, we use residue formula. 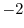 is the pole of order 2, by residue formula, we have
is the pole of order 2, by residue formula, we have
![$\displaystyle Res[-2] = \frac{1}{(2-1)!}\lim_{z \to -2}\frac{d}{dz}(z +2)^{2} \frac{e^z}{(z-1)(z+2)^2} = -\frac{4e^{-2}}{9} $](img1103.png)
2. Residue formula
The function  is analytic on and inside the single closed curve
is analytic on and inside the single closed curve  and monovalent, except for the finite number of points
and monovalent, except for the finite number of points
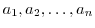 inside it. Then
inside it. Then
![$\displaystyle \int_{C}f(z) dz = 2\pi i\{Res[a_{1}] + Res[a_{2}] + \cdots + Res[a_{n}]\}$](img1105.png)
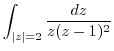 |
 |
![$\displaystyle 2\pi i\{Res[0] + Res[1]\} ($](img1107.png) z=0,1 are inside of z=0,1 are inside of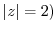 |
|
 |
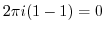 by by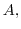 |
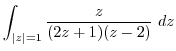 |
 |
![$\displaystyle 2\pi i Res[-\frac{1}{2}] ($](img1112.png) z=2 is not inside of z=2 is not inside of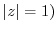 |
|
 |
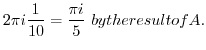 |
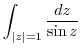 |
 |
![$\displaystyle 2\pi i Res[0] ($](img1116.png) z=0 is in z=0 is in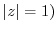 |
|
 |
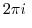 by by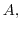 |
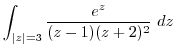 |
 |
![$\displaystyle 2\pi i (Res[1] + Res[-2]) ($](img1120.png) z=1,2 are in z=1,2 are in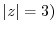 |
|
 |
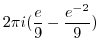 by by |
||
 |
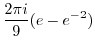 |
3.
(a) The circle 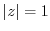 contains the singularity
contains the singularity 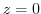 . So find
. So find ![$Res[0]$](img1125.png) . Then
. Then
![$\displaystyle Res[0]$](img1126.png) |
 |
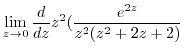 |
|
 |
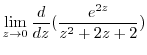 |
||
 |
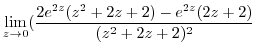 |
||
 |
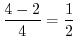 |
![$\displaystyle \int_{\vert z\vert=1}\frac{e^{2z}}{z^{2}(z^2 + 2z + 2)} dz = 2\pi i Res[0] = \pi i$](img1131.png)
(b) The circle 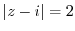 contains the singularity
contains the singularity 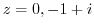 . Here
. Here ![$Res[0]$](img1125.png) is found by A. Thus, we find
is found by A. Thus, we find ![$Res[-1+i]$](img1133.png) .
.
![$\displaystyle Res[-1+i]$](img1134.png) |
 |
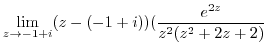 |
|
 |
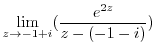 |
||
 |
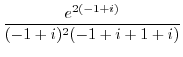 |
||
 |
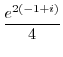 |
Thus by the residue theorem,
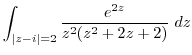 |
 |
![$\displaystyle 2\pi i (Res[0] + Res[-1+i])$](img1140.png) |
|
 |
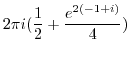 |
(c) The circle 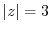 contains all singularity
contains all singularity
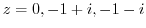 . Note that
. Note that
![$Res[0], Res[-1+i]$](img1143.png) are already found by A. So, we find
are already found by A. So, we find ![$Res[-1-i]$](img1144.png) .
.
![$\displaystyle Res[-1-i]$](img1145.png) |
 |
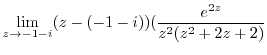 |
|
 |
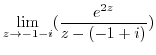 |
||
 |
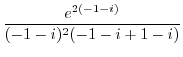 |
||
 |
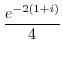 |
Then by the residue theorem,
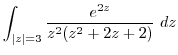 |
 |
![$\displaystyle 2\pi i (Res[0] + Res[-1+i] + Res[-1-i])$](img1151.png) |
|
 |
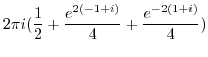 |
||
 |
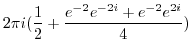 |
||
 |
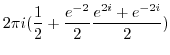 |
||
 |
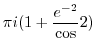 |