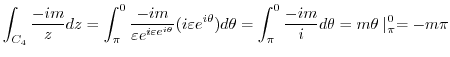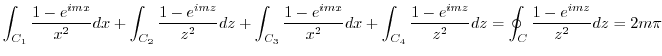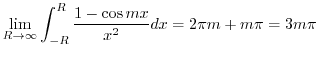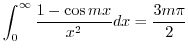Next: Index Up: Solution Previous: 5.2 Residue Index
1.
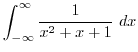
Let the closed curve  be the straight line connecting
be the straight line connecting 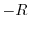 and
and 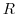 on the real axis, and
on the real axis, and 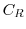 be the curveof the radius
be the curveof the radius 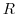 with center 0 connecting
with center 0 connecting 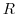 and
and 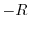 . Then the integral can be expressed as follows.
. Then the integral can be expressed as follows.
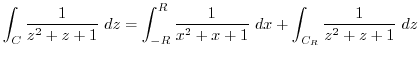
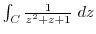 . The singularities are
. The singularities are
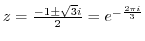 . But
. But
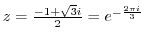 is inside of the curve
is inside of the curve  . Thus by the residue theorem, we have
. Thus by the residue theorem, we have
![$\displaystyle \int_{C}\frac{1}{(z^2 +1)(z^2 +4)} dz = 2\pi i(Res[e^{-\frac{2\pi i}{3}}])$](img1163.png)
![$\displaystyle Res[\frac{-1 + \sqrt{3}i}{2}]$](img1164.png) |
 |
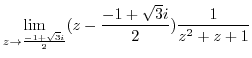 |
|
 |
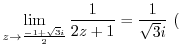 L'Hospital's rule L'Hospital's rule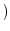 |
 , then
, then
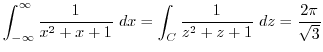
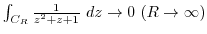 繧堤、コ縺99.
繧堤、コ縺99.
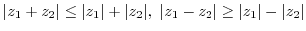
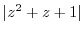 |
 |
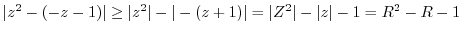 |
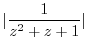 |
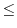 |
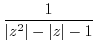 |
|
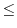 |
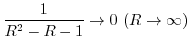 |
Let the closed curve  be the straight line connecting
be the straight line connecting 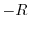 and
and 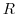 on the real axis, and
on the real axis, and 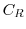 be the curve of the radius
be the curve of the radius 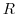 with center 0 connecting
with center 0 connecting 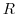 and
and 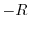 . Then the integral can be expressed as follows.
. Then the integral can be expressed as follows.
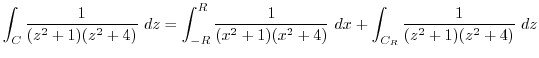
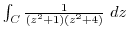 . The singularites are
. The singularites are
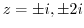 . But
. But 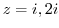 are only points inside of
are only points inside of  . Thus by the residue theorem, we can find the integral by
. Thus by the residue theorem, we can find the integral by
![$\displaystyle \int_{C}\frac{1}{(z^2 +1)(z^2 +4)} dz = 2\pi i(Res[i] + Res[2i])$](img1182.png)
![$\displaystyle Res[i] = \lim_{z \to i}(z - i)\frac{1}{(z^2 + 1)(z^2 + 4)} = \lim_{z \to i}\frac{1}{(z+i)(z^2 +4)} = \frac{1}{2i(3)} = \frac{1}{6i}$](img1183.png)
![$\displaystyle Res[2i] = \lim_{z \to 2i}(z - 2i)\frac{1}{(z^2 + 1)(z^2 + 4)} = \lim_{z \to 2i}\frac{1}{(z^2 + 1)(z + 2i)} = \frac{1}{-3(4i)} = \frac{-1}{12i}$](img1184.png)
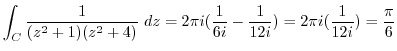
 , then
, then
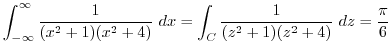
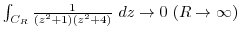 .
.
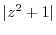 |
 |
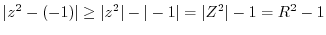 |
|
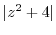 |
 |
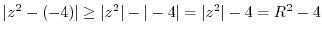 |
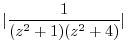 |
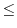 |
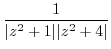 |
|
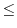 |
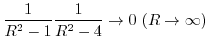 |
Thus,
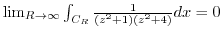 .
.
(c) It is a integral of a trigonometric function. So, we let
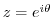 . Then the curve
. Then the curve  is a unit circle with the center at the origin. Next we write
is a unit circle with the center at the origin. Next we write
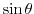 using
using  .
.
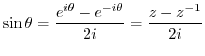
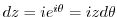 . Thus,
. Thus,
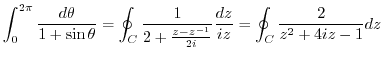
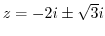 . But
. But
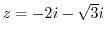 is outside of the curve
is outside of the curve  . So, we need to find the residue of
. So, we need to find the residue of
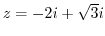 . Since
. Since
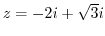 is the pole of the 1st order,
is the pole of the 1st order,
![$\displaystyle Res[-2i + \sqrt{3}i] = \lim_{z \to -2i + \sqrt{3}i}(z - (-2i + \s...
...^2 + 4iz -1}= \lim_{z \to -2i + \sqrt{3}i}\frac{2}{2z+4i} = \frac{1}{\sqrt{3}i}$](img1203.png)
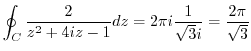
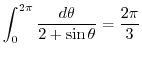
(d) To solve this integral, we conside the curve  represented by
represented by
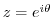 . Then
. Then
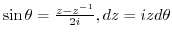 . Thus
. Thus
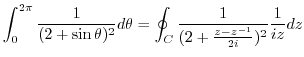
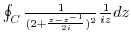 .
Since
.
Since
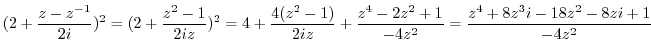
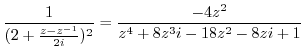
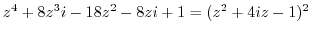 . Then the singularities are
. Then the singularities are
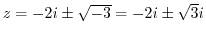 . Here,
. Here,
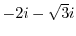 is otuside of the curve
is otuside of the curve  . So, we only need to find the residue of
. So, we only need to find the residue of
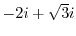 . Since,
. Since,
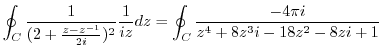
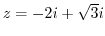 is the pole of the 2nd order. Thus,
is the pole of the 2nd order. Thus,
![$\displaystyle Res[-2i + \sqrt{3}i] = \lim_{z \to -(2-\sqrt{3})i}\left(\frac{4\p...
...{(z -(-2-\sqrt{3}i)^2}\right)' = \frac{32\sqrt{3}i}{48} = \frac{-2\sqrt{3}i}{3}$](img1216.png)
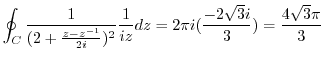
(e) Consider the straight line  connecting a point
connecting a point 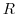 and
and 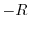 and the curve
and the curve 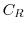 connecting a point
connecting a point 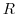 to
to 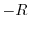 . Let
. Let  be the closed curve formed by
be the closed curve formed by  and
and 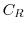 . Here, we conside the following integral.
. Here, we conside the following integral.
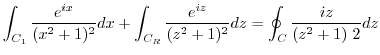
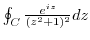 using the residue theorem.
using the residue theorem. 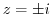 is the singular points. But
is the singular points. But 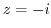 is outside of the curve
is outside of the curve  . Then we find the residue of
. Then we find the residue of 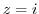 . Since
. Since 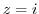 is the pole of the order 2, we have
is the pole of the order 2, we have
![$\displaystyle Res[i] = \lim_{z \to i}\left((z-i)^2\frac{e^{iz}}{(z+i)^2 (z-i)^2}\right)' = \frac{-ie^{-1}}{2}$](img1222.png)
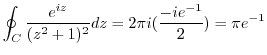
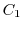 .
.
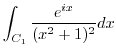 |
 |
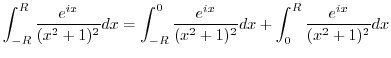 |
|
 |
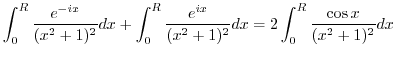 |
We integrate on 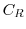 . We show
. We show
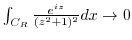 as
as
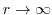 . To do so, we only need to show that there exists
. To do so, we only need to show that there exists 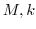 such that
such that
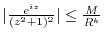 .
.
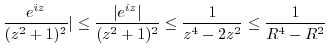
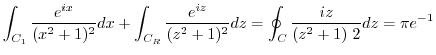
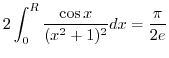
(f) Consider the straight line 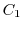 connecting a point
connecting a point 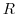 and
and 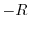 and the curve
and the curve 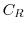 connecting a point
connecting a point 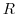 to
to 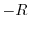 . Let
. Let  be the closed curve formed by
be the closed curve formed by  and
and 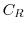 . Here, we conside the following integral.
. Here, we conside the following integral.
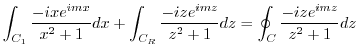
First we evaluate
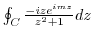 . Note that
. Note that 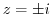 are the singularities. But
are the singularities. But 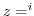 is outside of the curve
is outside of the curve  . Thus we only need to find the residue of
. Thus we only need to find the residue of 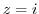 . Since
. Since 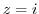 is the pole of the order 1. Thus,
is the pole of the order 1. Thus,
![$\displaystyle Res[i] = \lim_{z \to i}\frac{-ize^{imz}}{(z+i)(z-i)} = \frac{e^{-m}}{2i}$](img1237.png)
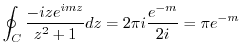
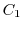 .
.
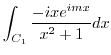 |
 |
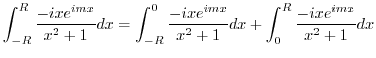 |
|
 |
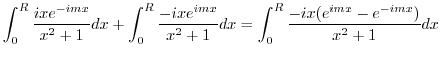 |
||
 |
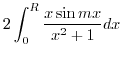 |
Finally, we consider the integral on 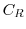 . We show that
. We show that
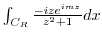 converges to 0 as
converges to 0 as
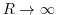 . For
. For 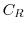 ,
,
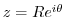 . Thus
. Thus
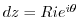 and
and
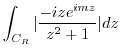 |
 |
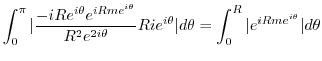 |
|
 |
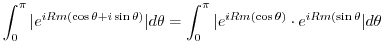 |
||
 |
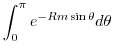 |
 and divide the above integral for
and divide the above integral for
![$[0, \frac{\pi}{2}]$](img1251.png) and
and
![$[\frac{\pi}{2},\pi]$](img1252.png) . Then
. Then
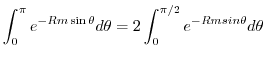
![$[0, \frac{\pi}{2}]$](img1251.png) ,
,
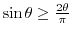 . Thu
. Thu
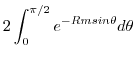 |
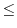 |
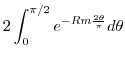 |
|
 |
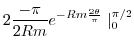 |
||
 |
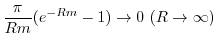 |
Thus,
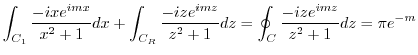
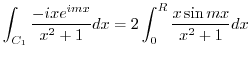
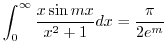
(g) To evaluate
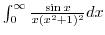 , we consider the straight line
, we consider the straight line 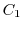 connecting point
connecting point
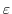 to
to 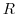 , the curve
, the curve 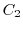 connecting
connecting 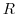 to
to 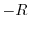 , the straight line
, the straight line 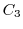 connecting
connecting 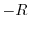 to
to
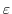 , the curve
, the curve 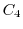 connecting
connecting
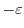 to
to
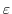 . The curve
. The curve  is composed of
is composed of
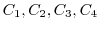 .
We consider the following integral.
.
We consider the following integral.
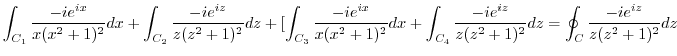
First by using the residue theorem, we evaluate
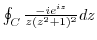 .
The singularities are
.
The singularities are
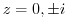 . But
. But 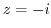 is outside of
is outside of  . So, we need to find the residue of
. So, we need to find the residue of 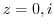 .
.
![$\displaystyle Res[0] = \lim_{z \to 0}\frac{-zie^{iz}}{z(z^2 + 1)^2} = -i$](img1273.png)
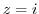 is the pole of the 2nd order. So,
is the pole of the 2nd order. So,
![$\displaystyle Res[i] = \lim_{z \to i}\left((z-i)^2\frac{-ie^{iz}}{z(z^2 + 1)^2}\right)' = \frac{-12ie^{-1}}{-16} = \frac{3i}{4e}$](img1274.png)
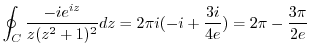
Next we evaluate the integral on  and
and  .
.
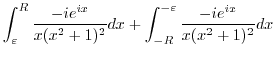
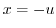 . Then
. Then 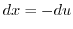 . For
. For
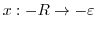 ,
,
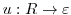 . Thus,
. Thus,
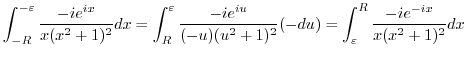
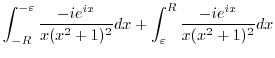 |
 |
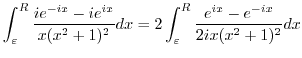 |
|
 |
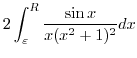 |
We evaluate the integral on 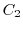 . Here we show
. Here we show
 converges to 0 as
converges to 0 as
 . Since
. Since
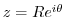 ,
,
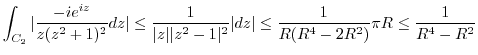
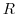 goes to
goes to 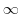 .
.
Lastly, we evaluate the integral on 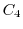 . Let
. Let
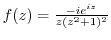 . Then Laurent expansion of
. Then Laurent expansion of  around
around 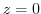 is
is
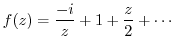
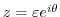 ,
,
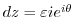 . Thus,
. Thus,
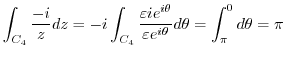
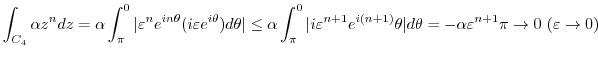
Putting all integrals together, we have
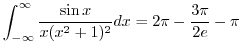
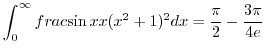
(g) To evaluate
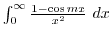 , we consider the straight line
, we consider the straight line  connecting point
connecting point
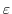 to
to 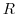 , the curve
, the curve 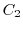 connecting
connecting 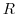 to
to 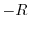 , the straight line
, the straight line 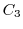 connecting
connecting 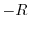 to
to
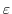 , the curve
, the curve 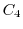 connecting
connecting
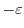 to
to
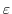 . The curve
. The curve  is composed of
is composed of
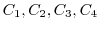 .
We consider the following integral.
.
We consider the following integral.
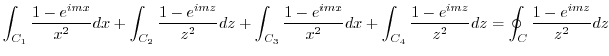
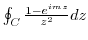 using the residue theorem.
Expand
using the residue theorem.
Expand
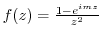 using Laurent expansion about
using Laurent expansion about 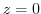 . Then
. Then
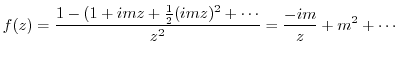
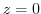 is the pole of the 1st order and the residue is
is the pole of the 1st order and the residue is 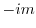 . Therefore,
. Therefore,
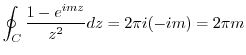
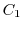 and
and 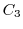 .
.
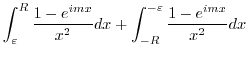
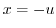 . Then
. Then 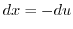 and
and
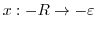 ,
,
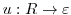 . Thus,
. Thus,
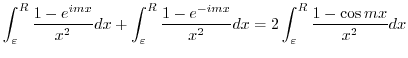
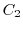 . We show that
. We show that
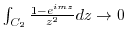 as
as
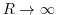 .
.
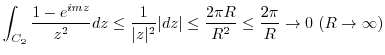
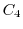 . Let
. Let
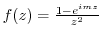 . Then expand
. Then expand  using Laurent expansion about
using Laurent expansion about 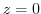 .
.
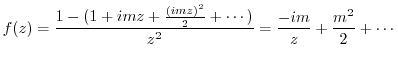
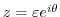 . Then
. Then
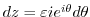 . Also,
. Also, 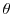 moves from
moves from 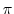 to 0. We evaluate this integral for the 1st term. Then
to 0. We evaluate this integral for the 1st term. Then