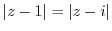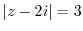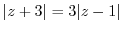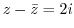Next: DeMoivre's theorem and Euler's Up: Complex numbers Previous: Complex numbers Index
A solution to the equation
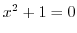 does not exist on
does not exist on 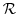 . Then, to be able to solve this equation, imaginary number
. Then, to be able to solve this equation, imaginary number 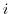 is introduced. In other words,
is introduced. In other words,
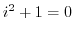 .
.
By incorporating the imaginary unit, a new system of numbers called complex number was created. Let 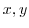 be real numbers. Then we express
be real numbers. Then we express
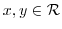 and
and 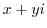 is called a complex number.
is called a complex number.
Complex number
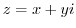 in orthogonal form,
in orthogonal form,
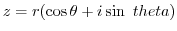 is called polar form. However,
is called polar form. However,
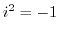 .
.
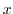 of complex number
of complex number
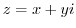 is called real part, and
is called real part, and
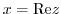 ,
, 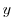 is imaginary part and it is represented by
is imaginary part and it is represented by
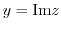 .
.
When
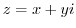 corresponds to the point
corresponds to the point 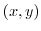 of the orthogonal coordinate form on the plane, this plane is complex plane or Gaussian plane
of the orthogonal coordinate form on the plane, this plane is complex plane or Gaussian plane
The absolute value of  is
is
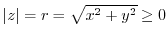 . The angle
. The angle 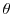 formed by the half line connecting the origin and
formed by the half line connecting the origin and  with the real axis is called argument, and the argument is
with the real axis is called argument, and the argument is
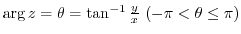 .
.
The conjugate complex number of  is represented by
is represented by
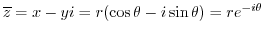 .
.
The operation of complex numbers is the same as the operation of real numbers, and 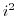 can be replaced with
can be replaced with 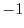 .
.
 on the complex plane
2. Prove the following theorem.
on the complex plane
2. Prove the following theorem.
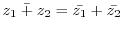
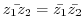
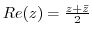
3. Prove the following inequality.
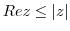
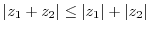
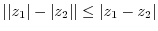
4. Express the following complex numbers in polar form.
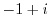
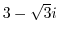
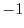
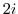
5. Draw a curve that satisfies the following equation.
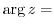 constant
constant
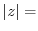 constant
constant