Next: 1.2 DeMoivre's theorem and Up: Solution Previous: Solution Index
1.
2.
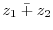 |
 |
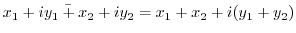 |
|
 |
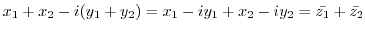 |
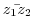 |
 |
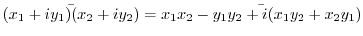 |
|
 |
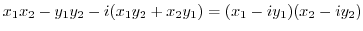 |
||
 |
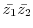 |
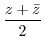 |
 |
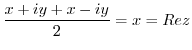 |
3.
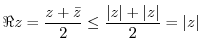
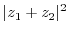 |
 |
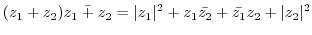 |
|
 |
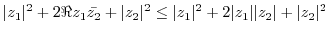 |
||
 |
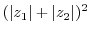 |
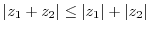
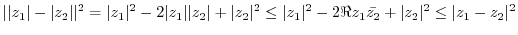
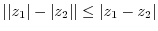
4.
(a) Cartesian coordinates to polar coordinates is given by
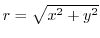 ,
,
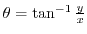 for
for
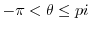 .
.
Write 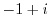 in polar coordinates, it is enough to find
in polar coordinates, it is enough to find
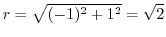 and
and
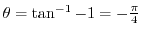 . Thus,
. Thus,
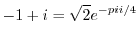
(b) Cartesian coordinates to polar coordinates is given by
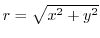 ,
,
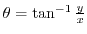 for
for
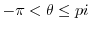 .
.
Write
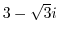 in polar coordinates, it is enough to find
in polar coordinates, it is enough to find
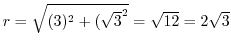 and
and
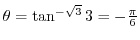 . Thus,
. Thus,
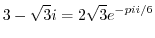
(c) Cartesian coordinates to polar coordinates is given by
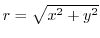 ,
,
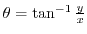 for
for
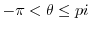 .
.
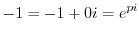
(d) Cartesian coordinates to polar coordinates is given by
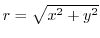 ,
,
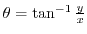 for
for
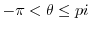 .
.
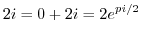
5.
(a) 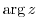 is the angle between the
is the angle between the 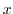 axis and the straight line drawn from the origin to the point
axis and the straight line drawn from the origin to the point  . Therefore, this is constant because the set of points
. Therefore, this is constant because the set of points  is a point that forms a constant angle with the
is a point that forms a constant angle with the 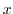 axis from the origin, so it is a straight line.
axis from the origin, so it is a straight line.
Alternate solution
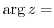 constant means that for some constant
constant means that for some constant 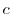 ,
,
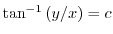 . Thus
. Thus
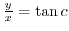 implies
implies
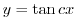 . Therefore, it is a straight line emitted from the origin.
. Therefore, it is a straight line emitted from the origin.
(b)
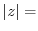 constant means that the distance from the origin is constant. Therefore, it is a circle.
constant means that the distance from the origin is constant. Therefore, it is a circle.
(c) 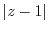 means that the distance from point 1. Also,
means that the distance from point 1. Also, 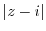 is the distance from the point
is the distance from the point 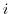 . A collection of points where the two are equal is a perpendicular bisector passing through point 1 and point
. A collection of points where the two are equal is a perpendicular bisector passing through point 1 and point 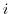 .
.
Alternate solution
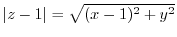 ,
,
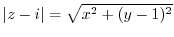 . Then rewrite
. Then rewrite
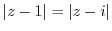 .
.
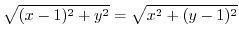
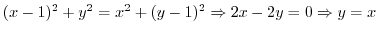
(d) 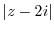 is the distance from point
is the distance from point 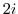 . Then
. Then
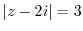 is the circle with the radius 3 centered at
is the circle with the radius 3 centered at 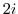 .
.
Alternate solutoin
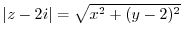 繧医j
Rewrite
繧医j
Rewrite
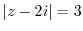
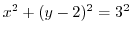
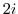 .
.
(e) 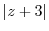 means
means
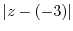 . Then it is the distance from the point
. Then it is the distance from the point 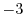 .
. 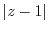 is the distance from the point
is the distance from the point 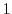 .
Thus
.
Thus
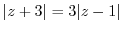 means that the distance from the point
means that the distance from the point 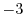 is 3 times the distance from the point
is 3 times the distance from the point 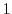 . Such a point draws a circle whose diameter is the point that internally divides the straight line connecting point-3 and point 1 into 3: 1 and the point that divides it outward. This circle is called Apollonius circle.
. Such a point draws a circle whose diameter is the point that internally divides the straight line connecting point-3 and point 1 into 3: 1 and the point that divides it outward. This circle is called Apollonius circle.
Alternate solution
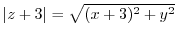 ,
,
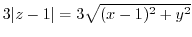 . Then rewrite
. Then rewrite
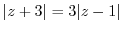
![$\displaystyle (x+3)^2 + y^2 = 9[(x-1)^2 + y^2]$](img463.png)
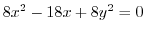
![$\displaystyle 8[(x - \frac{9}{8})^2 + y^2] = \frac{81}{8} $](img465.png)
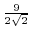 centered at
centered at
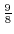 .
.