Next: Complex functions Up: Complex numbers Previous: complex numbers and complex Index
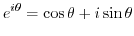
Proof The MacLaurin expansion of
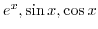 are
are
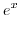 |
 |
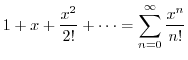 |
|
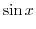 |
 |
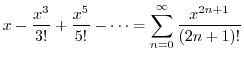 |
|
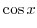 |
 |
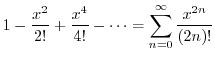 |
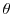 , we have
, we have
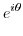 |
 |
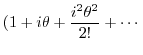 |
|
 |
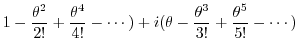 |
||
 |
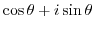 |
Properties
(1)
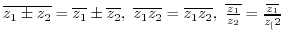
(2)
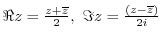
(3)
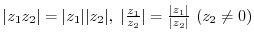
(4)
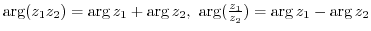
(5)
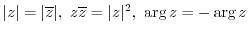
(6)
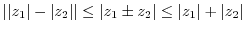
(7) 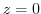 and
and 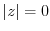 are equivalent (
are equivalent (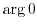 is undetermined)
is undetermined)
(8)
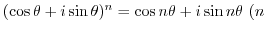 is constant
is constant De Moivre's theorem
(9)
Binary equation
De Moivre's theorem
(9)
Binary equation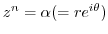 has the following solutions
has the following solutions
![$\displaystyle z_{k} = \sqrt[n]{r}\left(\cos{\frac{\theta + 2k\pi}{n}} + i\sin{\frac{\theta + 2k\pi}{n}}\right) (k = 0,1,2.\ldots,n-1)$](img64.png)
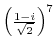
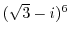
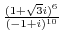
3. Solve the following equation.
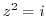
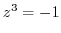
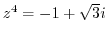
4. Express the followings in the form of 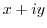 .
.
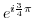
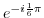
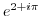
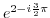
5. Express the followings in the polar form
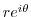 .
.
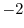
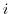
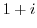
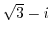
(6) Show that 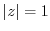 if and only if
if and only if
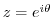 .
.