Next: Complex integration Up: Complex integration Previous: Complex integration Index
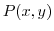 and
and 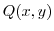 are real-valued functions of
are real-valued functions of 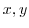 and continuous on every point on the curve
and continuous on every point on the curve  . Then the line integral of
. Then the line integral of
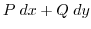 along the curve
along the curve  is defined by
is defined by
![$\displaystyle \int_{C} [P(x,y)\;dx + Q(x,y)\;dy]$](img313.png)
 is smooth and it is possible to parametrize by
is smooth and it is possible to parametrize by
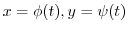 ,
,
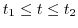 , then the line integral is given by
, then the line integral is given by
![$\displaystyle \int_{t_{1}}^{t_{2}}[P(\phi(t),\psi(t))\;dt + Q(\phi(t),\psi(t))\;dt]$](img316.png)
Let  be a single closed curve and
be a single closed curve and 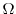 be a closed region consisting of its boundary and its interior. If functions
be a closed region consisting of its boundary and its interior. If functions
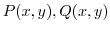 have continuouspartial derivatives on
have continuouspartial derivatives on 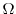 , then
, then
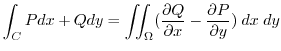
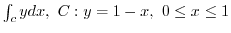
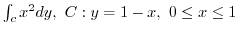
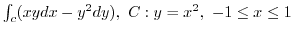
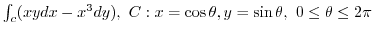
2. Find the following line integral for the parameter 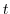
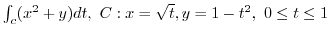
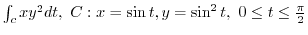
3. Using Green's theorem, evaluate the following line integral.
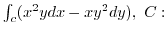 unit circle
unit circle
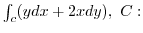 first quadrand quater circle
first quadrand quater circle