Next: 4.2 Complex integral Up: Solution Previous: 3.2 Analytic function Index
1. To find a complex integral, it is common to parametrize the curve  as
as
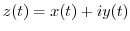 .
.
This curve is a straight line connecting a point 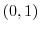 and a point
and a point 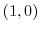 . Then we can parametrize this line such as
. Then we can parametrize this line such as
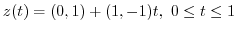 . Thus,
. Thus,
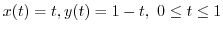 .
Therefore,
.
Therefore,
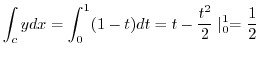
Alternate solution Since 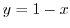 . we can integrate directly.
. we can integrate directly.
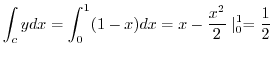
This curve is a straight line connecting a point 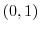 and a point
and a point 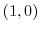 . Then we can parametrize this line such as
. Then we can parametrize this line such as
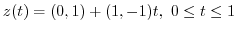 . Thus,
. Thus,
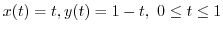 ,
, 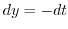 .
Therefore,
.
Therefore,
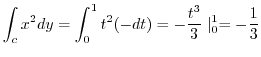
This is a curve 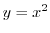 connecting
connecting 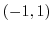 and
and 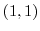 . Then we can parametrize this curve by
. Then we can parametrize this curve by
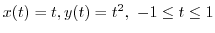 ,
, 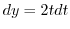 . Thus,
. Thus,
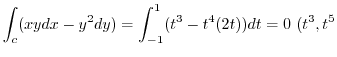 are odd function
are odd function
This curve is a circle of the radius 1 with the center at the origin. Then we can parametrize by
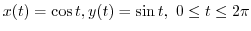 . Now
. Now
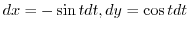 . Then
. Then
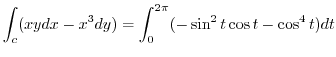
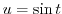 , then
, then
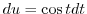 ,
,
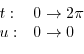 . Then
. Then
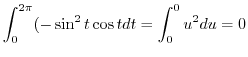
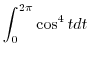 |
 |
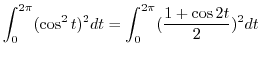 |
|
 |
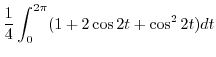 |
||
 |
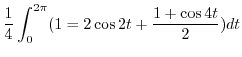 |
||
 |
![$\displaystyle \frac{1}{4}[\frac{3t}{2} + \cos{2t} + \frac{\sin{4t}}{8}\mid_{0}^{2\pi}]$](img801.png) |
||
 |
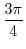 |
2.
(a) This curve is already parametrized.
Thus,
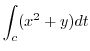 |
 |
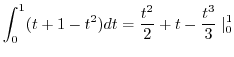 |
|
 |
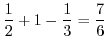 |
(b) This curve is already parametrized. Thus,
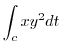 |
 |
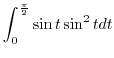 |
|
 |
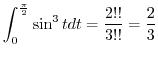 |
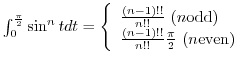
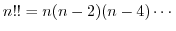 .
.
3. Green's theorem is the line integral of
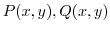 such that the partial derivatives are continuous on the simply connected domain
such that the partial derivatives are continuous on the simply connected domain 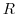 surrounded by a single closed curve
surrounded by a single closed curve  and it can be expressed as a double integral in the simply connected domain
and it can be expressed as a double integral in the simply connected domain 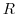 . That is
. That is
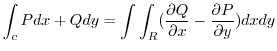
(a) Using Green's theorem, we have
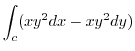 |
 |
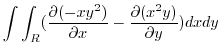 |
|
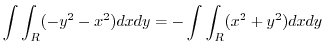 |
|||
 |
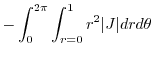 |
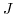 . Then
. Then
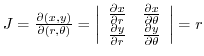 .
.
Thus,
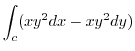 |
 |
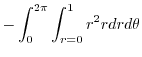 |
|
 |
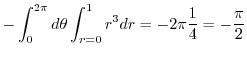 |
(b) Using Green's theorem, we have
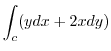 |
 |
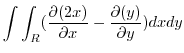 |
|
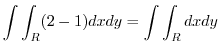 |
|||
 |
area of R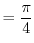 |