Next: 4.3 Cauchy's integral theorem Up: Solution Previous: 4.1 Line integral and Index
1. Parametrize a unit circle. Then
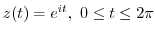 .
Thus
.
Thus
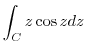 |
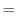 |
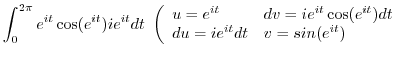 |
|
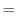 |
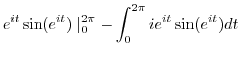 |
||
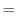 |
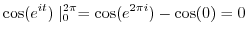 |
case1. The integral path is 0 to 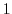 and
and 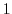 to
to 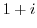 along the sides of the square.
along the sides of the square.
A straight line 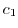 connecting 0 and
connecting 0 and 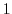 can be parametrized by
can be parametrized by
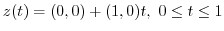 . Thus,
. Thus,
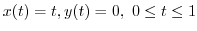 .
Therefore,
.
Therefore,
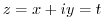 and
and
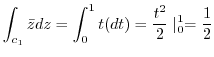
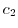 connecting
connecting 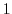 and
and 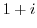 can be parametrized by
can be parametrized by
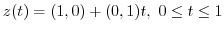 . Thus,
. Thus,
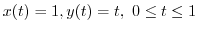 .
Therefore,
.
Therefore,
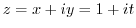 and
and
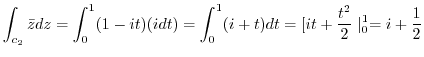
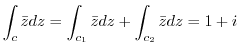
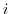 and
and 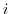 to
to 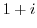 along the sides of the square.
along the sides of the square.
A straight line 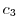 connecting 0 and
connecting 0 and 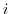 can be parametrized by
can be parametrized by
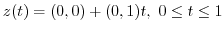 . Thus,
. Thus,
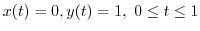 .
Therefore,
.
Therefore,
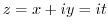 and
and
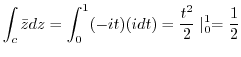
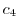 connecting
connecting 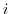 and
and 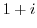 can be parametrized by
can be parametrized by
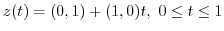 . Thus,
. Thus,
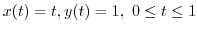 .
Therefore,
.
Therefore,
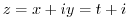 and
and
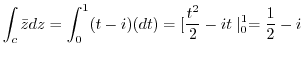
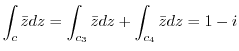
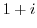 along the diagonal of the square.
along the diagonal of the square.
A straight line 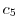 connecting 0 and
connecting 0 and 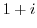 can be parametrized by
can be parametrized by
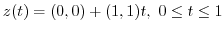 . Thus,
. Thus,
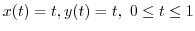 .
Therefore,
.
Therefore,
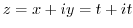 and
and