Next: Triple Integrals Up: Application of Double Integrals Previous: Surface Area Contents Index
| Understanding |
|---|
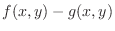 represents the height of the rectangular solid and represents the height of the rectangular solid and
 represents the base area. Thus represents the base area. Thus
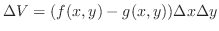 . .
|
Given a closed bounded region  and continuous functions
and continuous functions
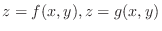 on
on  , and suppose that
, and suppose that
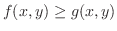 on
on  . Then the volume of solid bounded by the lines parallel to
. Then the volume of solid bounded by the lines parallel to 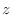 -axis through the boundary
-axis through the boundary
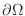 and the surfaces
and the surfaces 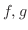 is given by
is given by
![$\displaystyle V = \iint_{\Omega}[f(x,y) - g(x,y)]dxdy $](img1420.png)
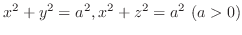 .
.
SOLUTION
Projection of the solid bounded by two cylinders onto 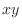 -plane is
-plane is
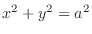 and
and 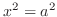 . Thus,
. Thus,
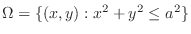 . Also
. Also
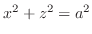 implies
implies
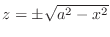 . Thus the upper surface is
. Thus the upper surface is
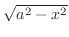 and the lower surface is
and the lower surface is
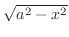 over
over  . From this, the volume of the solid is set up by
. From this, the volume of the solid is set up by
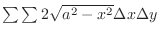 , where
, where
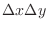 represents the small rectangle of base area and
represents the small rectangle of base area and
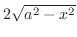 represents the height of a small solid cylinder.
Now use vertically simple region for
represents the height of a small solid cylinder.
Now use vertically simple region for  . Then
. Then
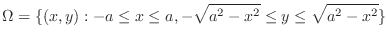
 |
 |
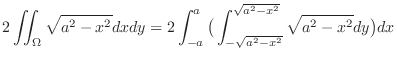 |
|
 |
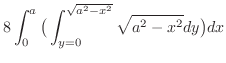 |
||
 |
![$\displaystyle 8\int_{0}^{a}\big[\sqrt{a^2 - x^2}y\big]_0^{\sqrt{a^2 - x^2}}dx$](img1434.png) |
||
 |
![$\displaystyle 8\int_{0}^{a}(a^2 - x^2)dx = 8\left[a^2 x - \frac{x^3}{3}\right ]_{0}^{a} = \frac{16a^3}{3}
\ensuremath{ \blacksquare}$](img1435.png) |
![% latex2html id marker 29793
\includegraphics[width=3.5cm]{SOFTFIG-5/reidai5-8.eps}](img1436.png)
Take a point in  and evaluate the value of
and evaluate the value of 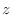 to find out which surfaces upper or lower surface.
to find out which surfaces upper or lower surface.
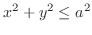 and
and
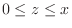 .
.
| Exercise5-8 |
|---|
![% latex2html id marker 29807
\includegraphics[width=3.5cm]{SOFTFIG-5/enshu5-8.eps}](img1439.png)
|
SOLUTION Note that the solid is bounded by the surface goes through the boundary of
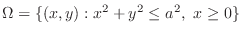 and parallel to the
and parallel to the 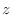 -axis, and the plane
-axis, and the plane 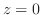 ,
, 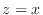 .
Using the polar coordinate to express
.
Using the polar coordinate to express  . Since
. Since
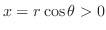 ,
,
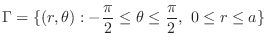
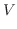 |
 |
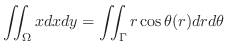 |
|
 |
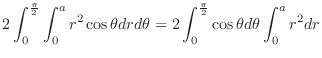 |
||
 |
![$\displaystyle 2\left[\sin{\theta}\right]_{0}^{\frac{\pi}{2}}\left[\frac{r^3}{3}\right]_{0}^{a} = \frac{2a^3}{3}\ensuremath{ \blacksquare}$](img1447.png) |
The limit of integration is constant, we can express the double integral as the product of two single integral.
(a) The region enclosed by
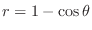
(b) Inside of the curve
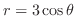 and outside of the curve
and outside of the curve
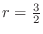 .
.
(c) Inside of the curve
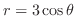 and outside of the curve
and outside of the curve
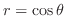
(a)
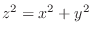 with
with
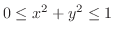 ,
, 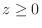 .
.
(b) 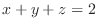 with
with
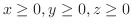 .
.
(c) 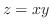 with
with
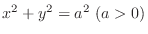 .
.
(a)
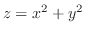 with
with 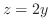
(b)
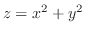 with
with
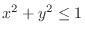
(a) Sphere
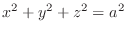 with the radius
with the radius 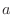 .
.
(b) 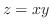 with
with
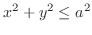
(c)
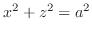 and
and
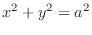 .
.
(d) The surface generated by rotating
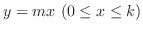 about
about  -axis for
-axis for 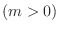 .
.
(a)
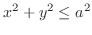 with
with
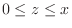
(b)
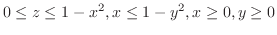 .
.
(c)
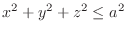 and
and
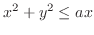 .
.
(d)
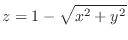 and
and 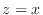 ,
, 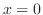 .
.