Next: Volume of Solid Up: Application of Double Integrals Previous: Area Contents Index
Suppose that
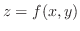 is a function of the class
is a function of the class 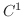 on the closed bounded region
on the closed bounded region  . Then
. Then
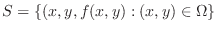
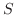 is given by
is given by

 is the projection of
is the projection of 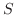 onto
onto 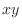 -plane.
-plane.
NOTE
The vector
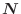 orthogonal to the small rectangle on the surface is given by
orthogonal to the small rectangle on the surface is given by
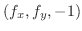 . Let
. Let 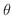 be the angle between the vector
be the angle between the vector
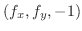 and the vector
and the vector
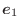 which is orthogonal to
which is orthogonal to 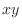 -plane. Then
-plane. Then
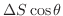 is equal to the
is equal to the
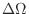 , a small area of
, a small area of 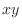 -plane.Thus,
-plane.Thus,
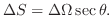 Note that
Note that
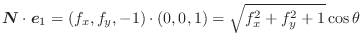
Thus we can express the surface area 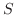 as the following double integral.
as the following double integral.

| Dot Product |
|---|
The dot product of a vector
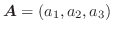 and a vector and a vector
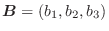 is given by is given by
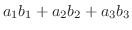 and is written as and is written as
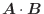 . .
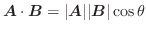 . .
|
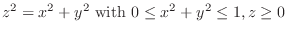
![% latex2html id marker 29576
\includegraphics[width=3.5cm]{SOFTFIG-5/reidai5-7.eps}](img1377.png)
SOLUTION To find the surface area, we need to find the  which is a projection of the surface
which is a projection of the surface
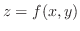 .
Since
.
Since 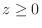 , the surface is
, the surface is
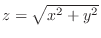 . Now the region
. Now the region  is given by
is given by
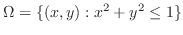 . Thus, the surface area is given by the following double integral
. Thus, the surface area is given by the following double integral
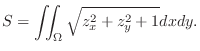
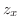 |
 |
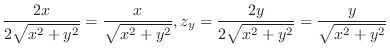 |
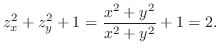
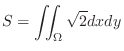
 is a circular region of the radius 1. Thus by using the polar coordinate,
is a circular region of the radius 1. Thus by using the polar coordinate,
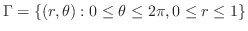
 |
 |
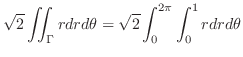 |
|
 |
![$\displaystyle \sqrt{2} \int_{0}^{2\pi}\left[\frac{r^2}{2}\right]_{0}^1 d\theta ...
...{2}}{2}\left[\theta\right]_{0}^{2\pi} = \sqrt{2}\pi \ensuremath{ \blacksquare}$](img1388.png) |
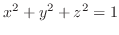 cut by cylinder
cut by cylinder
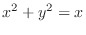 .
.
| Exercise5-7 |
|---|
![% latex2html id marker 29626
\includegraphics[width=3.5cm]{SOFTFIG-5/enshu5-7.eps}](img1391.png)
|
SOLUTION
Note that
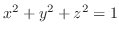 implies
implies
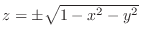 . Then find the following surface area and double it
. Then find the following surface area and double it
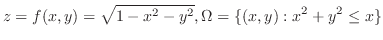
 |
 |
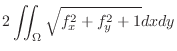 |
|
 |
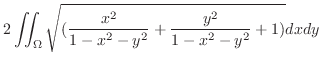 |
||
 |
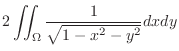 |
| Check |
|---|
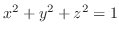 implies implies
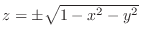 . .
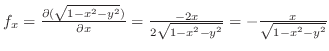 , ,
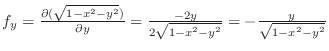
|
Let
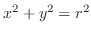 ,
,
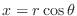 . Then
. Then
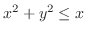 is transformed to
is transformed to
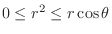 . Thus,
. Thus,
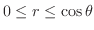 . Therefore,
. Therefore,
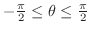
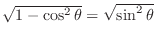 Then for
Then for
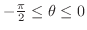 ,
,
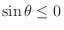 . Thus
. Thus
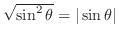 .
.
Now using polar coordinate,  is mapped into
is mapped into
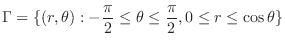
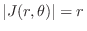 ,
,
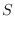 |
 |
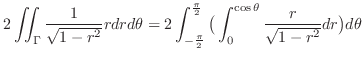 |
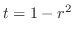 Then
Then
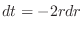 ,
,
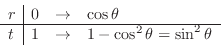 .
Thus,
.
Thus,
 |
 |
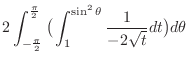 |
|
 |
![$\displaystyle 2\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\big(\int_{1}^{\sin^{2}{\th...
...\pi}{2}}^{\frac{\pi}{2}} \big[-t^{\frac{1}{2}}\big]_1^{\sin^{2}{\theta}}d\theta$](img1411.png) |
||
 |
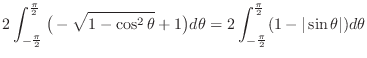 |
||
 |
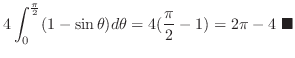 |