Next: Application of Double Integrals Up: Multiple Integrals Previous: Change of Variables Contents Index
The double integrals treated so far are the case where a function is bounded on the bounded region. Now consider the case where  is not bounded.
is not bounded.
The sequence of bounded closed regions
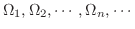 in
in  satisfy
satisfy
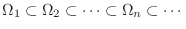
 is a subset of
is a subset of
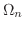 .
Then if
.
Then if  is integrable on the region
is integrable on the region
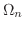 ,
,
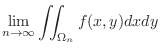
 is integrable on
is integrable on  and define
and define
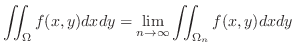
| Understanding |
|---|
If a function
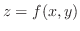 is not bounded on a region, then we say the double integral is improper integral of the 1st kind. If the region is not bounded, then we say the double integral is improper integral of the 2nd kind. If a function is not bounded on unbounded region, then we say the double integral is improper integral of the 3rd kind. is not bounded on a region, then we say the double integral is improper integral of the 1st kind. If the region is not bounded, then we say the double integral is improper integral of the 2nd kind. If a function is not bounded on unbounded region, then we say the double integral is improper integral of the 3rd kind.
|
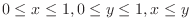 .
.
![% latex2html id marker 29165
\includegraphics[width=3.5cm]{SOFTFIG-5/reidai5-5-1.eps}](img1267.png)
SOLUTION
1. Using horizontally simple region, we have
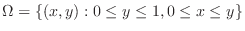 . Then
. Then
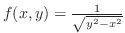 is discontinuous at
is discontinuous at 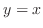 . Thus let
. Thus let
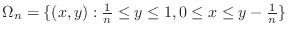 . Then
. Then
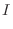 |
 |
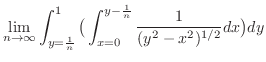 |
|
 |
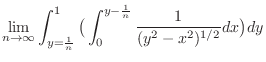 |
||
 |
 |
Create 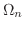 so that
so that
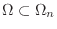 as
as 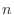 goes to infinity.
goes to infinity.
2. The region  is not bounded. So, consider the sequence of closed bounded regions
is not bounded. So, consider the sequence of closed bounded regions
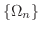 .
.
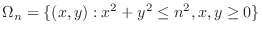
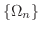 is given by the figure 5.19.
For
is given by the figure 5.19.
For
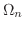 , use the polar coordinate
, use the polar coordinate
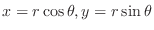
| Check |
|---|
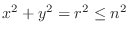 implies that implies that 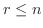 . Since . Since
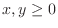 , ,
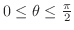 . .
|
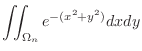 |
 |
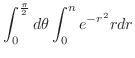 |
|
 |
![$\displaystyle \frac{\pi}{2}\left[-\frac{e^{-r^2}}{2}\right ]_{0}^{n} = \frac{\pi}{4}(1 - e^{-n^2})$](img1284.png) |
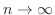 , we find
, we find 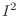 and
and
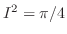

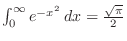 |
|---|
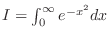 , ,
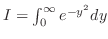 . Then . Then
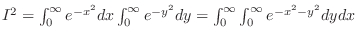 implies implies
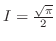 . .
|
Consider a function  is not bounded on
is not bounded on  .
.
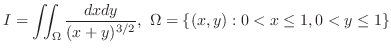
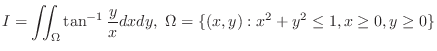
| Exercise5-5-2. |
|---|
Create 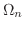 so that so that  is a subset of is a subset of 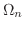 as as 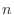 goes to infinity. goes to infinity.
|
SOLUTION
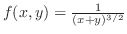 is discontinuous at
is discontinuous at 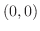 . Then create
. Then create 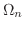 so that
so that 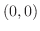 is not included in
is not included in 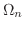 .
.
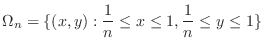
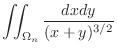 |
 |
![$\displaystyle \int_{1/n}^{1}dx\int_{1/n}^{1} \frac{dy}{(x+y)^{3/2}} = \int_{1/n}^{1}\left[-\frac{2}{(x+y)^{1/2}}\right ]_{\frac{1}{n}}^{1}dx$](img1299.png) |
|
 |
![$\displaystyle 2\int_{1/n}^{1}[(x+\frac{1}{n})^{-\frac{1}{2}} - (x+1)^{-\frac{1}{2}} ]dx$](img1300.png) |
||
 |
![$\displaystyle 2\left[2(x+\frac{1}{n})^{\frac{1}{2}} - 2(x+1)^{\frac{1}{2}}\right ]_{\frac{1}{n}}^{1}$](img1301.png) |
||
 |
![$\displaystyle 4[2(1+\frac{1}{n})^{\frac{1}{2}} - \sqrt{2} - (\frac{2}{n})^{\frac{1}{2}}]$](img1302.png) |
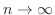 we can find
we can find
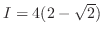

| Check |
|---|
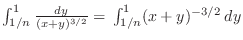 . .
This is the integral with respect to  . Thus we treat . Thus we treat  as a constant. Now as a constant. Now
![$\int_{1/n}^{1} (x+y)^{-3/2}\:dy = \left[-2(x+y)^{-\frac{1}{2}}\right]_{\frac{1}{n}}^1$](img1305.png)
|
| Exercise5-5-2. |
|---|
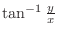 is not bounded at is not bounded at  . Using polar coordinate transformation . Using polar coordinate transformation
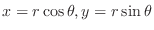 , the region , the region  can be covered by taking can be covered by taking 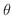 goes from 0 to goes from 0 to
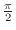 and the distance from the pole ranges from 0 to and the distance from the pole ranges from 0 to 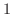 . Thus, . Thus,
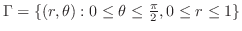 . .
|
2.
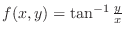 is bounded except on
is bounded except on  -axis.
-axis.
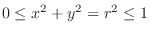 ,
,
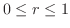 . Since
. Since
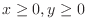 ,
,
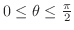 . Thus
. Thus  maps to
maps to
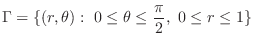
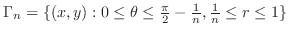 . Then,
. Then,
![% latex2html id marker 29362
\includegraphics[width=4cm]{SOFTFIG-5/enshu5-5-2-1.eps}](img1314.png)
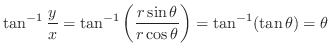
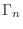 . Thus,
. Thus,
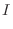 |
 |
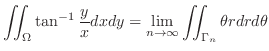 |
|
 |
![$\displaystyle \lim_{n \to \infty}\int_{\theta = 0}^{\frac{\pi}{2}-\frac{1}{n}}\...
...{\frac{\pi}{2}-\frac{1}{n}}\big(\left[\frac{r^2}{2}\right]_{\frac{1}{n}}^1\big)$](img1318.png) |
||
 |
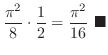 |
Exercise A
Exercise B
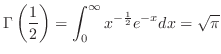 D
D