Next: Multiple Integrals Up: Partial Differentiation Previous: Implicit Functions Contents Index
 takes extrema at
takes extrema at 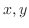 given the constraint
given the constraint
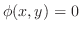 , Then let
, Then let
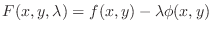
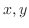
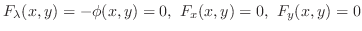
| Understanding |
|---|
The constraint is
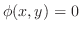 . Thus the set of real numbers . Thus the set of real numbers
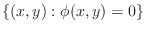 is a closed bounded set. Thus if is a closed bounded set. Thus if
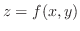 is continuous, then is continuous, then
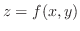 takes either the maximum or minimum. takes either the maximum or minimum.
|
| Implicit Function |
|---|
 is the class is the class 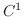 , ,
1. 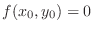
2. 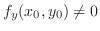 . .
|
NOTE Under the constraint
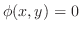 , we find the extrema of
, we find the extrema of  . As
. As
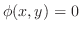 , if
, if
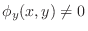 , then we can find the implicit function
, then we can find the implicit function 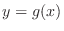 satissfying
satissfying
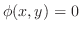 .
If a function
.
If a function
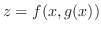 takes the extrema at
takes the extrema at
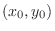 , then
, then
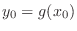 and
and 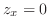 . Thus
. Thus
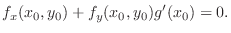
 by
by  . Then
. Then
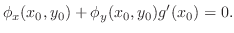
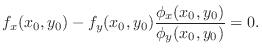
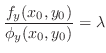
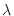 satisying
satisying
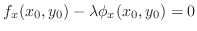
| Check |
|---|
Solve for 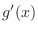 , we have , we have
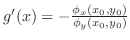 . Now substitute . Now substitute 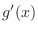 into into
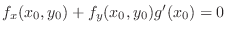 . Then . Then
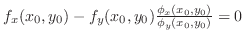 . .
|
| Gradient |
|---|
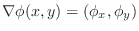 is called gradient. is called gradient.
|
If we think of this theorem geometrically.
Since
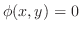 , the vector
, the vector
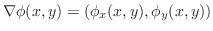 is orthogonal to the curve
is orthogonal to the curve
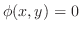 . Let
. Let 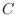 be the curve defined by the constraint
be the curve defined by the constraint
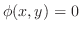 and
and
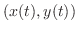 is a point on
is a point on 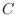 . If a function
. If a function
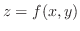 takes the extrema at
takes the extrema at
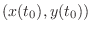 , then
, then
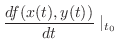 |
 |
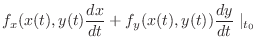 |
|
 |
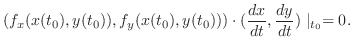 |
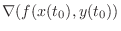 is orthogonal to the curve
is orthogonal to the curve 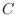 . Then
. Then
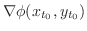 and
and
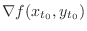 are parallel. Thus, there exists
are parallel. Thus, there exists 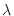 so that
so that
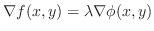
| Parallel |
|---|
Note that
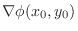 and and
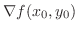 are parallel, then are parallel, then
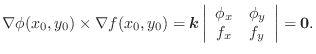
|
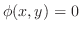 .
.
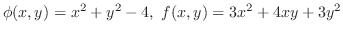
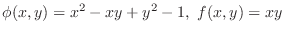
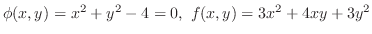 . Let
. Let
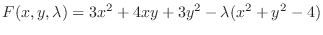
Using 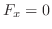 ,
, 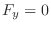 , and
, and
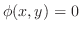 , first find a
, first find a 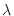 .
.
SOLUTION
| Check |
|---|
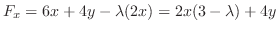
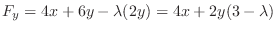
|
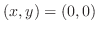 does not satisfy the equation 4.5. Then the condition that the equations 4.6 and 4.6 have solutions
does not satisfy the equation 4.5. Then the condition that the equations 4.6 and 4.6 have solutions  not equal to
not equal to
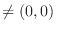 ,
,
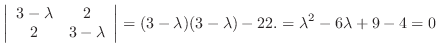
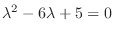 and
and
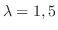 .
.
For
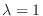 , by the equation 4.6,
, by the equation 4.6,
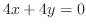 and
and 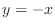 . Substitute
. Substitute 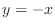 into the equation 4.5, we have
into the equation 4.5, we have
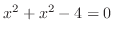 and
and
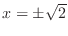 . Since
. Since 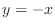 , we have
, we have
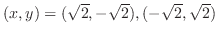 .
With these
.
With these 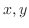 , the value of
, the value of
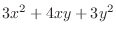 is 4.
is 4.
For
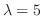 , by the equation 4.6,
, by the equation 4.6,
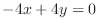 and
and 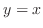 . Substitute
. Substitute 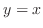 into the equation 4.5. Then
into the equation 4.5. Then
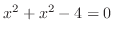 which implies
which implies
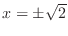 . Since
. Since 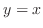 ,
,
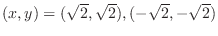 . With these
. With these  , the value of
, the value of
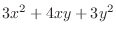 is
is 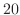 .
.
| Check |
|---|
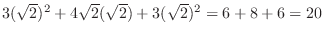
|
On the other hand,
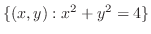 is closed bounded region, and on this region,
is closed bounded region, and on this region,
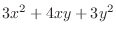 is continuous, thus takes the extrema. these are also local extrema. Thus by the result above, the extrema must be 4 or 20. Therefore, the maximum value is 20 and the minimum value is 4
is continuous, thus takes the extrema. these are also local extrema. Thus by the result above, the extrema must be 4 or 20. Therefore, the maximum value is 20 and the minimum value is 4

2. Note that
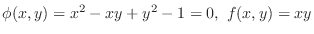 . Then let
. Then let
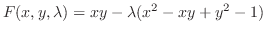
| Check |
|---|
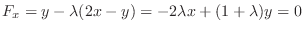
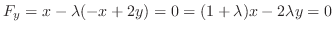
|
| System of Equation |
|---|
A sysytem of 1st order linear equation
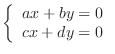 has no solution if and only if has no solution if and only if
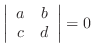
|
Now
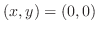 does not satisy the equation 4.7. Then the condition for the equation 4.8), (4.8) has the solution
does not satisy the equation 4.7. Then the condition for the equation 4.8), (4.8) has the solution
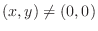 ,
,
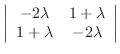 |
 |
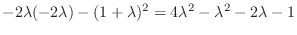 |
|
 |
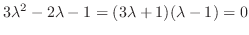 |
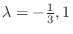 .
.
For
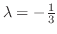 , by the equation 4.8,
, by the equation 4.8,
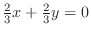 and
and 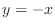 . Substitute
. Substitute 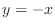 into the equation 4.7. Then
into the equation 4.7. Then
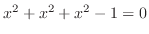 . From this,
. From this,
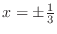 . Since
. Since 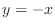 ,
,
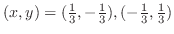 .
Now the value of
.
Now the value of 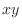 for these values of
for these values of 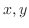 is
is
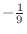 .
.
For
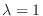 , by the equation 4.8,
, by the equation 4.8,
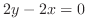 and
and 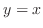 . Substitute
. Substitute 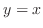 into the equation4.7. Then
into the equation4.7. Then
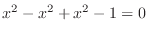 . From this,
. From this, 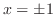 . Since
. Since 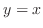 ,
,
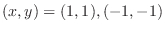 . Now the valuesof
. Now the valuesof 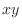 for these values of
for these values of 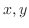 is
is 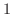 .
.
On the other hand,
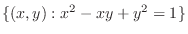 is closed bounded region, and on this region,
is closed bounded region, and on this region,
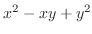 is continuous, thus takes the extrema. these are also local extrema. Thus by the result above, the extrema must be
is continuous, thus takes the extrema. these are also local extrema. Thus by the result above, the extrema must be
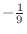 or 1. Therefore, the maximum value is 1 and the minimum value is
or 1. Therefore, the maximum value is 1 and the minimum value is
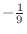

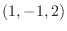 to the surface
to the surface
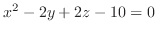 .
.
SOLUTION
Let 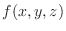 be the distance from the point
be the distance from the point 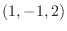 to an arbitrary point on the surface. Then minimize
to an arbitrary point on the surface. Then minimize 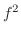 .
.
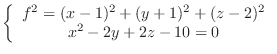
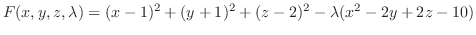
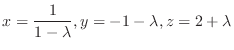
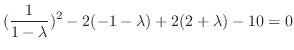
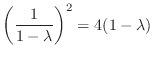
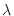 to get
to get
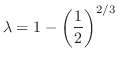
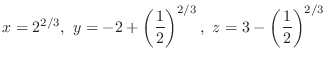
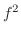 is not bounded above. Thus this is the local minimum. Furthermore, it is only one. Thus, it is the minimum value
is not bounded above. Thus this is the local minimum. Furthermore, it is only one. Thus, it is the minimum value

| Check |
|---|
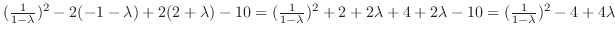
|
| Check |
|---|
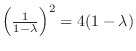 , ,
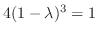 . .
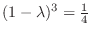 . .
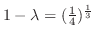 . .
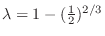 . .
|
 with the constraint
with the constraint
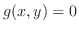 .
.
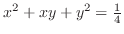 .
.
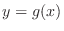 implicitly defined by the following functions .
implicitly defined by the following functions .
 with the constraint
with the constraint
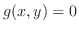 .
.
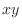 for if the point
for if the point
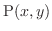 moves on the line
moves on the line
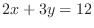 .
.
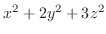 for if the point
for if the point
 moves on the surface
moves on the surface
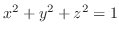 .
.