4.9 Lagrange's multiplier

1.

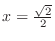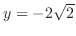(a) at $x = \frac{\sqrt{2}}{2}$, $y = -2\sqrt{2}$ is local minimum，at 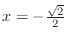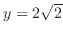$x = -\frac{\sqrt{2}}{2}$, $y = 2\sqrt{2}$ is local maximum．

(b) at 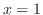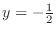$x = 1$, $y = -\frac{1}{2}$ is local maximum，at $x = -1$, $y = \frac{1}{2}$ is local minimum．

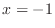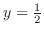(c) at $x = 2 \sqrt[3]{2}$, $y = 2\cdot2^{\frac{2}{3}}$ is local minimum．

2.

(a) maximum 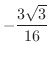$${-\frac{3\sqrt{3}}{16}}$$, maximum 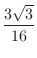$${\frac{3\sqrt{3}}{16}}$$(b) at 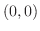$(0,0)$, minimum value 0, at 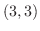$(3,3)$, maximum value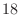 $18$

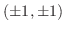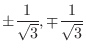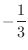
(c) at $(\pm 1, \pm 1)$, maximum value 1, at $${\pm \frac{1}{\sqrt{3}}, \mp \frac{1}{\sqrt{3}}}$$, minimum value $${-\frac{1}{3}}$$

3.

$6$

4.

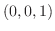at $(0,0,1)$, maximum value 3， at 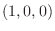$(1,0,0)$ minimum value 1