Next: Lagrange Multiplier Up: Conditional Extrema Previous: Conditional Extrema Contents Index
From the equation
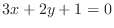 , we can find
, we can find  in terms of
in terms of  . In other words, we can find
. In other words, we can find
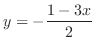 . In general, given a quadratic function
. In general, given a quadratic function  , if
, if 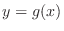 always satisfies
always satisfies
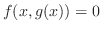 , then we say the equation
, then we say the equation 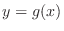 is an implicit function determined by the equation
is an implicit function determined by the equation
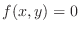 .
.
| Understanding |
|---|
Finding the implicit function 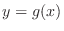 determined by the equation determined by the equation
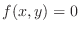 is the same as solving the equation is the same as solving the equation
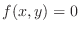 for for  . But for some type of . But for some type of 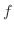 and some and some  , there may not be a , there may not be a  satisfying the equation satisfying the equation
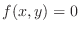 . .
|
 is the class
is the class 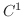 at
at
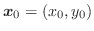 in the region
in the region 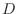 . If
. If
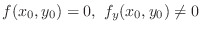
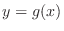 determined by
determined by
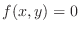 in the neighborhood of
in the neighborhood of 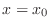 which satisfies
which satisfies
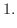 |
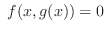 |
||
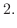 |
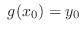 |
||
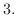 |
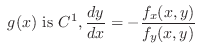 |
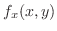 is a funciton of
is a funciton of 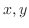 and
and  is a function of
is a function of  . Thus we have the following figure.
. Thus we have the following figure.
Thus,
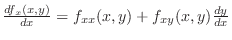
NOTE In the neighborhood of the point satisfying
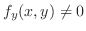 , the implicit function
, the implicit function  exists and the implcit function is differentiable. Thus the total diffetential of
exists and the implcit function is differentiable. Thus the total diffetential of 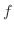 is
is
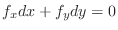
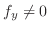 ,
,
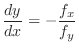
 , we have
, we have
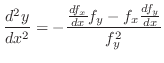
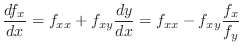
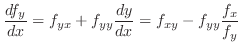
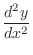 |
 |
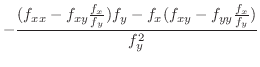 |
|
 |
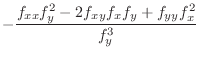 |
| Implicit Functions |
|---|
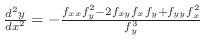 is called 2nd order derivative of implicit function is called 2nd order derivative of implicit function
|
 such as
such as
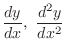 deteremined by
deteremined by
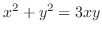
SOLUTION
Set
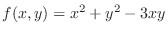 and take total differential of
and take total differential of  ,
,
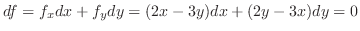
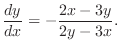
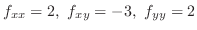 ,
,
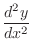 |
 |
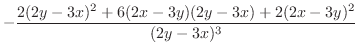 |
|
 |
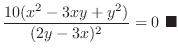 |
A problem of finding a differentiation of an implicit function is solved by taking total differentiatial
| Check |
|---|
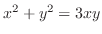
|
 such as
such as
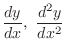 deteremined by
deteremined by
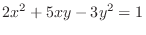
| Exercise4-19 |
|---|
Since
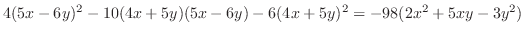 and and
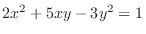 . .
|
SOLUTION Set
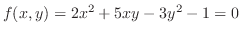 and find total differential of
and find total differential of  . Then
. Then
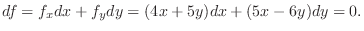
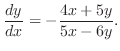
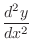 |
 |
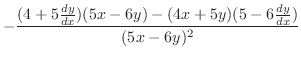 |
|
 |
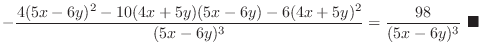 |
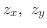 for the implicit function
for the implicit function
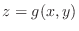 determined by the equation
determined by the equation
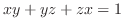 .
.
By writing
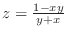 , we can find
, we can find
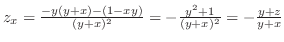 .
.
SOLUTION
For
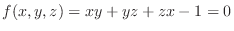 , set
, set
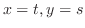 . Then,
. Then,
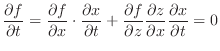
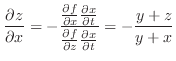
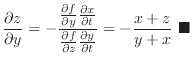
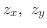 for the implicit function
for the implicit function
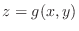 determined by the equation
determined by the equation
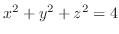 .
.
SOLUTION
For
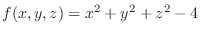 , set
, set
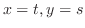 .
.
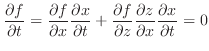
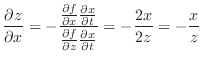
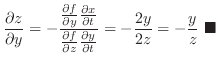
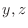 of
of  is determined by the equations
is determined by the equations
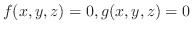 , then,
, then,
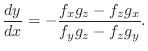
| Theorem4-9 |
|---|
To find
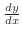 , we first find , we first find 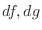 and then eliminate and then eliminate 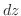 . .
|
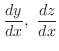 for the implicit functions
for the implicit functions 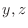 of
of  determined by the equations
determined by the equations
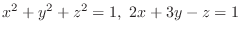 .
.
SOLUTION
Let
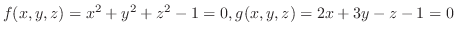 . Then totally differentiate
. Then totally differentiate 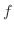 and
and 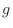 to get
to get
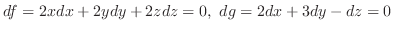
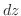 to get
to get
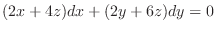
| Check |
|---|
From the equations
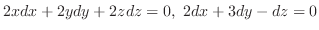 , we delete , we delete 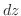 by adding by adding
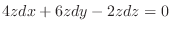 to the first equation, to the first equation,
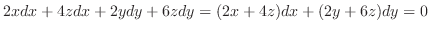 . .
|
Thus,
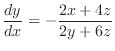
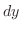 to get
to get
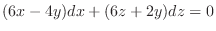
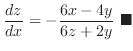
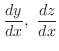 for the implicit functions
for the implicit functions 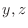 of
of  determined by the equations
determined by the equations
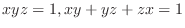 .
.| Check |
|---|
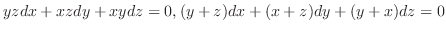 . Eliminate . Eliminate 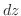 by multiplying by multiplying 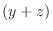 to the former equation and multiplyimg to the former equation and multiplyimg 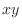 to the latter equation. to the latter equation.
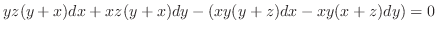 . Simplifying, . Simplifying,
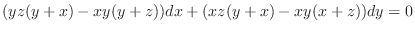
|
SOLUTION Let
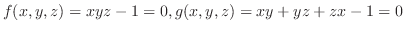 . Then find total derivatives.
. Then find total derivatives.
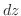 .
.
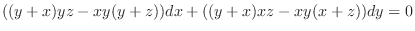
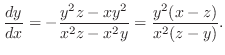
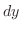 .
.
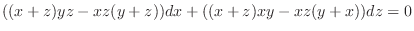
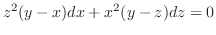
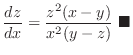
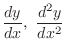 for the implicit functions
for the implicit functions  of
of  determined by the following functionsD
determined by the following functionsD
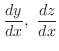 for the implicit functions
for the implicit functions 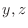 of
of  determined by the following functionsD
determined by the following functionsD
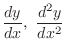 for the implicit function
for the implicit function  of
of  determined by the following equations.
determined by the following equations.
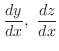 for the implicit function
for the implicit function 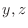 of
of  determined by the following equations.
determined by the following equations.
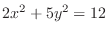 at the point
at the point
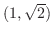 .
.
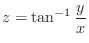 at the point
at the point
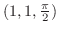 DFind the equation of the normal line through
DFind the equation of the normal line through
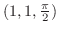 .
.
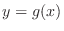 implicitly defined by the following equationsD
implicitly defined by the following equationsD