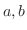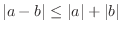Next: Functions Up: Introduction Previous: Inequalities Contents Index
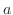 is given by
is given by
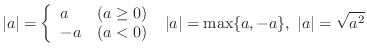
We first consider the inequality
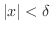
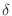 is some positive number. Now
is some positive number. Now
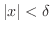 can be thought of the points on the number line whose distance from the origin is less than
can be thought of the points on the number line whose distance from the origin is less than 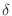 . Thus,
. Thus,
\colorbox{calc-color}{ \begin{minipage}{0.9\textwidth} \begin{equation} |x| < \delta \Leftrightarrow -\delta < x < \delta \label{eq:ineq1-1} \end{equation} \end{minipage} }
Next
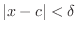 can be thought of the points whose distance from the point
can be thought of the points whose distance from the point 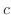 is less than
is less than 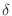 . Thus,
. Thus,
Lastly
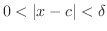 can be thought of
can be thought of
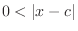 and
and
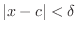 The first inequality is
The first inequality is 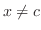 . Thus
. Thus
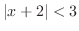
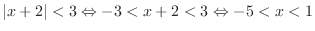
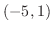

Let
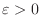 . Then
. Then
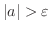 can be think of the distance from the origin to
can be think of the distance from the origin to 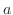 is larger than
is larger than
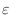 Thus
Thus
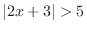
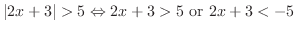
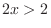 . Thus
. Thus 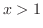 . By the second inequalitywe have
. By the second inequalitywe have 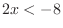 . Thus
. Thus 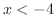 From this, the solution is
From this, the solution is
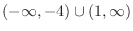

One of the popular inequalities of calculus is the triangle inequality
 ,
,
|
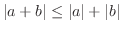
|
Traiangle Inequality 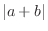 can be thought of the length of hypotenuse of triangle and
can be thought of the length of hypotenuse of triangle and 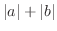 can be thought of the sum of the length of oppsite and adjacent
can be thought of the sum of the length of oppsite and adjacent
PROOF If you think of 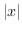 as
as
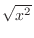 , then the proof is easy. Note that
, then the proof is easy. Note that
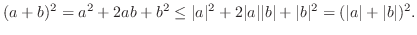
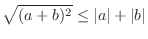
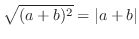

Here is another inequality used in calculus.
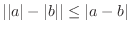
![[*]](crossref.png) renshu0-2-2
renshu0-2-2
![[*]](crossref.png) renshu0-2-4
renshu0-2-4