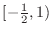Next: Inequalities and absolute value Up: Introduction Previous: Real Numbers Contents Index
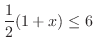
SOLUTION To solve this inequality, we first multiply both sides of inequality by 2.
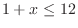
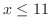
![$(-\infty, 11]$](img58.png)

Basic Technique To solve inequality, first eliminate the outside factor
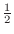
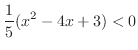
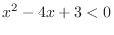
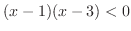
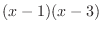 becomes 0 at 1 and 3Then we make circle on the number line at 1 and 3. Then we have 3 separated parts
becomes 0 at 1 and 3Then we make circle on the number line at 1 and 3. Then we have 3 separated parts
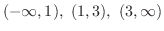
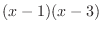 does not change.
Thus we have
does not change.
Thus we have
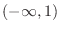 |
![${\rm sgn}[(x-1)(x-3)] = (-)(-) = +$](img67.png) |
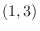 |
![${\rm sgn}[(x-1)(x-3)] = (+)(-) = -$](img69.png) |
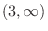 |
![${\rm sgn}[(x-1)(x-3)] = (+)(+) = +$](img71.png) |
From this we obtain 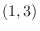

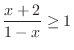
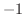 to both sides of the inequality to get rid of 1.
to both sides of the inequality to get rid of 1.

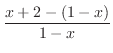 |
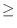 |
0 | |
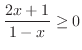 |
Now we would like to get rid of the denominator 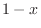 . But if we multiply
. But if we multiply 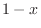 to get rid of the denominator, then we have to be careful about the sign of
to get rid of the denominator, then we have to be careful about the sign of 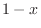 . Thus insteadwe multiply
. Thus insteadwe multiply 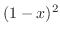 . Then we have
. Then we have
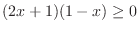
Inequality in Fraction To solve the inequality with the fraction, first transpose an expression to get one side of inequality is 0. Then eliminate the denominator by multiplying the square of the denominator
Now as above, the product
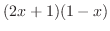 becomes 0 at
becomes 0 at
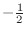 and 1Then we make circle on the number line at
and 1Then we make circle on the number line at
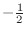 and 1 Next note that the equality only holds at the point where the numerator is 0. From this we fill the circle at
and 1 Next note that the equality only holds at the point where the numerator is 0. From this we fill the circle at
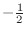 From this the number line can be separated by 3 parts
From this the number line can be separated by 3 parts
![$\displaystyle (-\infty, -\frac{1}{2}], [-\frac{1}{2},1), (1, \infty)$](img83.png)
![$(-\infty, -\frac{1}{2}]$](img84.png) |
![${\rm sgn}[(2x+1)(1-x)] = (-)(+) = -$](img85.png) |
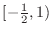 |
![${\rm sgn}[(2x+1)(1-x)] = (+)(+) = +$](img87.png) |
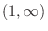 |
![${\rm sgn}[(2x+1)(1-x)] = (+)(-) = -$](img89.png) |
Therefore, the solution is