Next: Arc length Up: Application of Definite Integrals Previous: Area Contents Index
 -axis. Let
-axis. Let 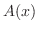 be the cross-sectional area . Then the volume of the solid corresponds to
be the cross-sectional area . Then the volume of the solid corresponds to
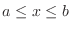 is given by
is given by
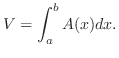
| Volume |
|---|
Let 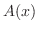 be the cross-sectional area perpendicular to the be the cross-sectional area perpendicular to the  -axis. Then the volume is approximated by the -axis. Then the volume is approximated by the
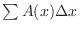 and is equal to and is equal to
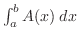 . .
|
NOTE Partition ![$[a,b]$](img1050.png) into subintervlas
into subintervlas
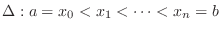
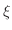 be an element in
be an element in
![$[x_{i-1},x_{i}]$](img2810.png) . Now let the base area be
. Now let the base area be 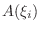 and the height be
and the height be 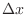 . Then
letting
. Then
letting 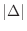 approaches 0. the Riemann sum converges to
approaches 0. the Riemann sum converges to
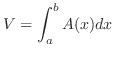 .
.
There are two ways to find the volume of solid generated by rotating the region. One way to find the volume is to rotate cross-sectional area perpendiculat to the totating axis. The other way to find the volume is to use cylindrical shell.
If
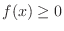 for all
for all  in
in ![$[a,b]$](img1050.png) , then the volume given by rotating the region
, then the volume given by rotating the region
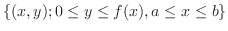 around
around  -axis is given by
-axis is given by
![$\displaystyle V = \int_{a}^{b} \underbrace{\pi y^{2}}_{\rm Cross-sectional area} dx = \int_{a}^{b} \pi [f(x)]^{2} dx $](img3285.png)
Volume When rotate about  -axis, take the thickness as
-axis, take the thickness as 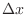 and the area of circle with the radius
and the area of circle with the radius  . Then the volume of small disk is
. Then the volume of small disk is
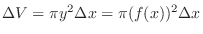 .
.
Let 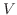 be the volume of solid rotating the region
be the volume of solid rotating the region
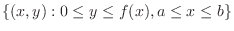 around
around  -axis. Consider the cylindrical shell with the radius
-axis. Consider the cylindrical shell with the radius  and the height
and the height  . Then the surface area of cylinder is
. Then the surface area of cylinder is 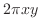 .
Thus
.
Thus
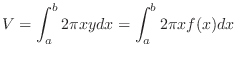
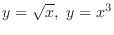 around the
around the  -axis.
-axis. 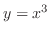 and
and
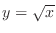 . Then
. Then
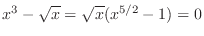 . Thus
. Thus 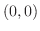 and
and 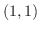 are the intersection points.
Slice the solid by the plane perpendicular to the rotating axis. Then the cross section becomes washer shape. Thus the cross-sectional area at
are the intersection points.
Slice the solid by the plane perpendicular to the rotating axis. Then the cross section becomes washer shape. Thus the cross-sectional area at  is
is
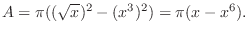
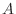 by the thickness
by the thickness 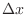 to get the volume
to get the volume 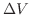 .
.
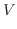 |
 |
![$\displaystyle \pi \int_{0}^{1}(x - x^6)\; dx = \pi \left[\frac{x^2}{2} - \frac{x^7}{7}\right]_{0}^{1}$](img3301.png) |
|
 |
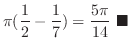 |
| Common Mistakes |
|---|
Let 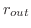 be the radius of outer circle of a washer and be the radius of outer circle of a washer and 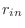 be the radius of innner circle of washer. Then the area of washer is be the radius of innner circle of washer. Then the area of washer is
![$\pi[(r_{out})^2 - (r_{in})^2]$](img3306.png) not not
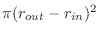 . .
|
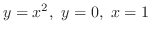 around
around  -axis.
-axis.
![\includegraphics[width=6cm]{SOFTFIG-3/Fig3-4.eps}](img3309.png)
SOLUTION
Slice the solid by the plane perpendicular to the  -axis. Then the cross section is washer shape. Now the area of the washer is
-axis. Then the cross section is washer shape. Now the area of the washer is
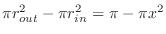 . Thus the volume of washer with thickness
. Thus the volume of washer with thickness 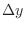 is given by
is given by
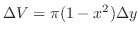 .
.
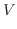 |
 |
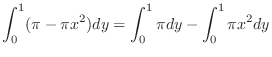 |
|
 |
![$\displaystyle \pi - \pi \int_{0}^{1} y dy = \pi - \pi \left[\frac{y^2}{2} \right ]_{0}^{1} = \frac{\pi}{2}\ensuremath{ \blacksquare}$](img3314.png) |
 be the radius of the cylindrical shell and
be the radius of the cylindrical shell and  be the height. Then the surface area becomes
be the height. Then the surface area becomes 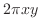 . Now the volume of cylindrical shell with the thickness
. Now the volume of cylindrical shell with the thickness 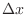 is given by
is given by
 . Thus
. Thus
![$\displaystyle V = \int_{0}^{1}2 \pi x y dx = \int_{0}^{1} 2 \pi x x^2 dx = 2 \pi \left[\frac{x^4}{4}\right ]_{0}^{1} = \frac{\pi}{2}
\ensuremath{ \blacksquare}
$](img3316.png)