Area

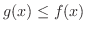Area Suppose that $g(x) \leq f(x)$ for all $x \in [a,b]$ . Let the region $A$

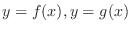be bounded by two curves $y = f(x),y = g(x)$

and lines

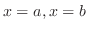. Then

$\displaystyle A = \int_a^b[f(x) - g(x)]\:dx$

**Figure 3.18:** Area
$\includegraphics[width=3.5cm]{SOFTFIG-3/area.eps}$

NOTE Partition $[a,b]$

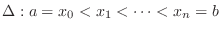
$\displaystyle \Delta : a = x_{0} < x_{1} < \cdots < x_{n} = b$

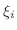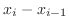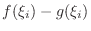For each subinterval $[x_{i-1},x_{i}]$ , we take point $\xi_{i}$ . Now consider therectangle with the base $x_{i} - x_{i-1}$ and the height $f(\xi_{i}) - g(\xi_{i})$ .

$\displaystyle \sum_{i=1}^{n}\underbrace{[f(\xi_{i}) - g(\xi_{i})]}_{\rm height}\underbrace{(x_{i}-x_{i-1}) }_{\rm base}.$

Now let $\Delta$ get smaller. Then the Riemann sum converges to

$\displaystyle A = \int_{a}^{b}[f(x) - g(x)]dx$

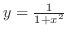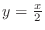Example 3..21 Find the area of the region bounded by $y = \frac{1}{1+x^2}$ , $y = \frac{x}{2}$ , and $y$

-axis.

**Figure 3.19:** Example3-21
$% latex2html id marker 48157 \includegraphics[width=3.5cm]{SOFTFIG-3/reidai3-21_gr3.eps}$

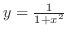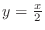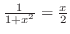SOLUTION First find the intersetin of $y = \frac{1}{1+x^2}$ and $y = \frac{x}{2}$ . Letting $\frac{1}{1+x^2} = \frac{x}{2}$ , simplifying 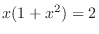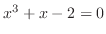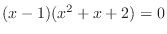$x(1+x^2) = 2$ , $x^3 + x - 2 = 0$ . $(x-1)(x^2 + x + 2) = 0$ , we have 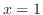$x = 1$ . Now consider the small rectangle with the base 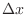$\Delta x$ and the height 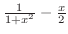$\frac{1}{1+x^2} - \frac{x}{2}$ . Therefore,

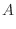$\displaystyle A$	$\displaystyle =$	$\displaystyle \int_0^1 \big(\frac{1}{1+x^2} - \frac{x}{2}\big)dx = \left[\tan^{-1}{x} - \frac{x^2}{4}\right]_0^1$
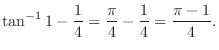	$\displaystyle =$	$\displaystyle \tan^{-1}{1} - \frac{1}{4} = \frac{\pi}{4} - \frac{1}{4} = \frac{\pi -1}{4}.$

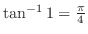
$\tan^{-1}{1} = \frac{\pi}{4}$
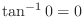$\tan^{-1}{0} = 0$ .

Exercise 3..21 Find the area of the region bounded by the following curves.

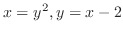
$\displaystyle x = y^{2}, y = x-2$

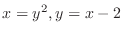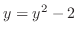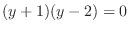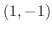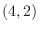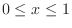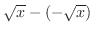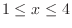SOLUTION Use a vertically long rectangle or horizontally long rectangle to make a Riemannsum. Find the intersection of $x = y^2, y = x -2$ . Then $y = y^2 - 2$ which implies $(y +1)(y-2) = 0$ . Thus $(1,-1)$ and $(4,2)$ are the intersetions. 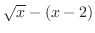Now note that for $0 \leq x \leq 1$ , the height of small rectangle is given by $\sqrt{x} - (-\sqrt{x})$ and for $1 \leq x \leq 4$ , the height of small rectangle is given by $\sqrt{x} - (x - 2)$ . Thus

$\displaystyle A$	$\displaystyle =$	$\displaystyle \int_{0}^{1}2\sqrt{x}dx + \int_{1}^{4}[\sqrt{x} - (x - 2)] dx = \left[\frac{4}{3}x^{3/2} \right ]_{0}^{1}$
	$\displaystyle +$	$\displaystyle \left[\frac{2}{3}x^{3/2} - \frac{x^2}{2} + 2x\right]_{1}^{4} = \frac{4}{3} + \frac{3}{2}[4^{3/2} - 1] -\frac{1}{2}[4^2 - 1] + 2[4-1]$
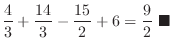	$\displaystyle =$	$\displaystyle \frac{4}{3} + \frac{14}{3} - \frac{15}{2} + 6 = \frac{9}{2}\ensuremath{ \blacksquare}$

**Figure 3.20:**
$\includegraphics[width=4.5cm]{SOFTFIG-3/Fig3-11-1.eps}$

Alternative SOLUTION Find the intersection of 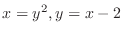$x = y^2, y = x -2$ . Since 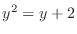$y^2 = y + 2$ , we have 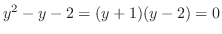$y^2 - y - 2 = (y + 1)(y - 2) = 0$ . Then 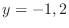$y = -1, 2$ . Now consider horizontally long rectangle with the side length 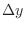$\Delta y$ and the width 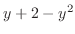$y+2 - y^2$ . Then

$\displaystyle A = \int_{-1}^{2}(y + 2 - y^2)dy = \left[\frac{y^2}{2} + 2y - \frac{y^3}{3} \right]_{-1}^{2} = \frac{9}{2} \ensuremath{ \blacksquare}$