Next: ANSWERS Up: Application of Definite Integrals Previous: Volume Contents Index
arc length
Let  be class
be class 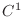 . Then the arc length
. Then the arc length 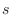 of a curve
of a curve 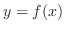 , where
, where
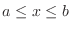 is given by
is given by
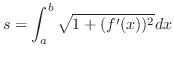
NOTE Partition ![$[a,b]$](img1050.png)
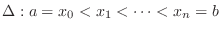
 be the point
be the point
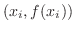 . Then connect the points
. Then connect the points
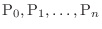 by a straight line to get
by a straight line to get
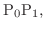
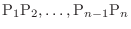 .
.
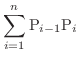
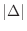 get smaller, if the Riemann sum converges to
get smaller, if the Riemann sum converges to 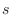 , then we say
, then we say 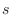 arc length of
arc length of 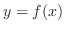 for
for
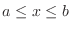 .
.
| Smooth Curve |
|---|
If  is the class is the class 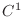 , the curve of a function , the curve of a function 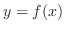 is called smooth. is called smooth.
|
Arc Length
Note that the length of the line segment is decomposed with 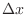 and
and 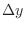 . Then
. Then
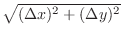 .
.
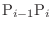 |
 |
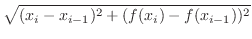 |
|
 |
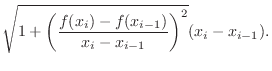 |
| Check |
|---|
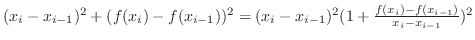 . .
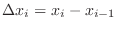 . .
|
Note that since  is the class
is the class 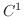 , use the mean value theorem,
, use the mean value theorem,
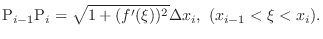
 is
is
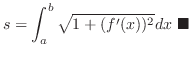
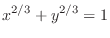
SOLUTION Let
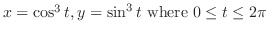 . Then the small arc length
. Then the small arc length 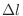 is given by
is given by
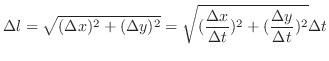
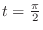 . Thus
. Thus
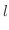 |
 |
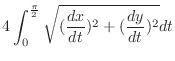 |
|
 |
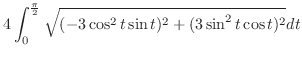 |
||
 |
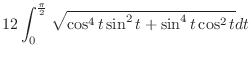 |
||
 |
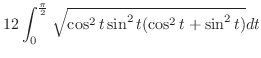 |
||
 |
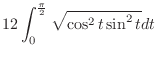 |
||
 |
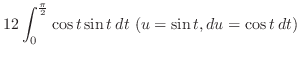 |
||
 |
![$\displaystyle 12 \int_0^1 udu = 12 \left[\frac{u^2}{2}\right]_0^1 = 12\cdot \frac{1}{2} = 6\ensuremath{ \blacksquare}$](img3348.png) |
If the curve is hard to represent by 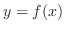 , then it is better to use parametric representation.
For parametric representation
, then it is better to use parametric representation.
For parametric representation
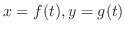 , if
, if
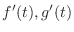 are continuous on
are continuous on 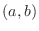 and not equal to 0 simultaneously, then the curve is smooth.
Since
and not equal to 0 simultaneously, then the curve is smooth.
Since
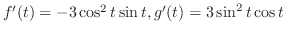 ,
, 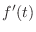 and
and 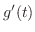 are 0 at
are 0 at
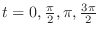 simultaneously.
Arc length If the curve of a function is not smooth, then it is not the class
simultaneously.
Arc length If the curve of a function is not smooth, then it is not the class 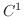 . In this case, we find the arc length of the curve which is smooth.
. In this case, we find the arc length of the curve which is smooth.
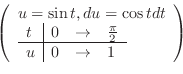 .
.
| Check |
|---|
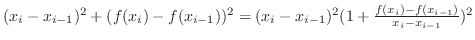 . .
 . .
|
Note that since  is the class
is the class 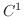 , use the mean value theorem,
, use the mean value theorem,
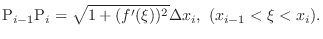
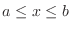 is
is
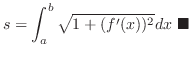
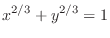
SOLUTION Let
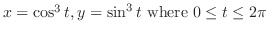 . Then the small arc length
. Then the small arc length 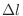 is given by
is given by
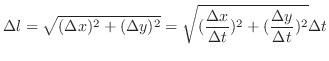
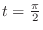 . Thus
. Thus
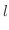 |
 |
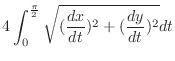 |
|
 |
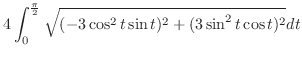 |
||
 |
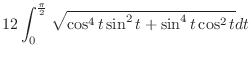 |
||
 |
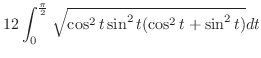 |
||
 |
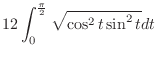 |
||
 |
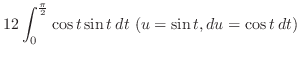 |
||
 |
![$\displaystyle 12 \int_0^1 udu = 12 \left[\frac{u^2}{2}\right]_0^1 = 12\cdot \frac{1}{2} = 6\ensuremath{ \blacksquare}$](img3348.png) |
If the curve is hard to represent by 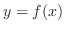 , then it is better to use parametric representation.
For parametric representation
, then it is better to use parametric representation.
For parametric representation
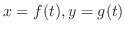 , if
, if
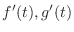 are continuous on
are continuous on 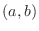 and not equal to 0 simultaneously, then the curve is smooth.
Since
and not equal to 0 simultaneously, then the curve is smooth.
Since
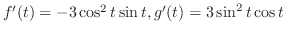 ,
, 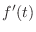 and
and 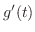 are 0 at
are 0 at
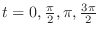 simultaneously.
Arc length If the curve of a function is not smooth, then it is not the class
simultaneously.
Arc length If the curve of a function is not smooth, then it is not the class 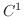 . In this case, we find the arc length of the curve which is smooth.
. In this case, we find the arc length of the curve which is smooth.
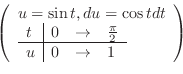 .
.
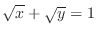
SOLUTION Parametrize by
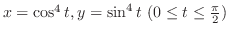 .
.
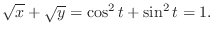
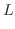 |
 |
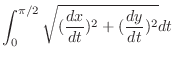 |
|
 |
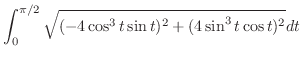 |
||
 |
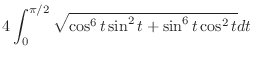 |
||
 |
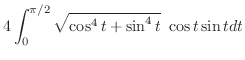 |
||
 |
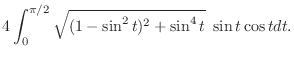 |
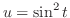 . Then
. Then
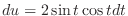 and
and
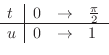
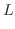 |
 |
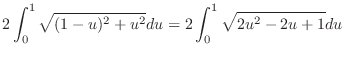 |
|
 |
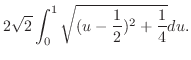 |
| Check |
|---|
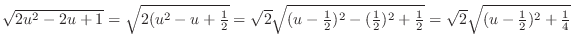 . .
|
Let
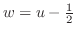 . Then
. Then 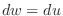 and
and
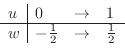
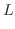 |
 |
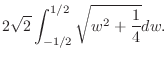 |
Now use the following integral formula,
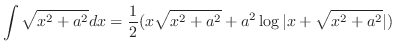
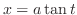 . Then
. Then
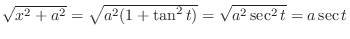 . Also,
. Also,
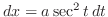 ,
,
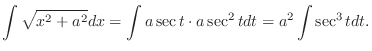
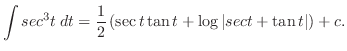
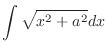 |
 |
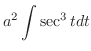 |
|
 |
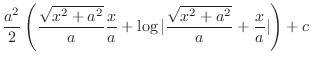 |
||
 |
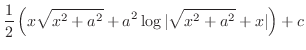 |
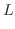 |
 |
![$\displaystyle 2\sqrt{2}\cdot \frac{1}{2}\left[(w\sqrt{w^2 + \frac{1}{4}} + \frac{1}{4}\log\vert w + \sqrt{w^2 + \frac{1}{4}}\vert)\right]\mid_{-1/2}^{1/2}$](img3387.png) |
|
 |
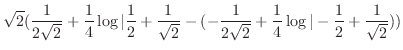 |
||
 |
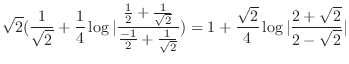 |
||
 |
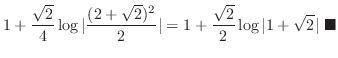 |
|
Exercise A
|
 -axis
-axis
(a)
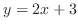 from
from 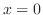 to
to 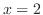 (b)
(b)
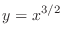 from
from 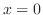 to
to 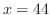 (c)
(c)
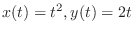 from
from 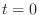 to
to
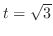
(d)
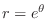 from
from
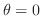 to
to
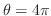
|
Exercise B
|
 -axis
-axis
(b)
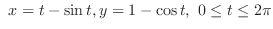 and
and  -axis
-axis