Next: Limit of Functions Up: Functions Previous: Inverse Trigonometric Functions Contents Index
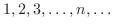 , there corresponds unique real number
, there corresponds unique real number
 term.
term.
NOTE Once the  th term is found, all terms can be derived. Thus we call the
th term is found, all terms can be derived. Thus we call the  th term general term.
th term general term.
Arithmetic sequence A sequence  whose difference between the consecutive terms is constant is called Arithmetic sequence. Note that we can express
whose difference between the consecutive terms is constant is called Arithmetic sequence. Note that we can express
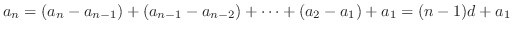 .
Geometric sequence A sequence
.
Geometric sequence A sequence  whose ratio of consecutive terms is constant is called geometric sequence. Note that
whose ratio of consecutive terms is constant is called geometric sequence. Note that
 .
.
Bounded sequence A sequence  is called bounded above if there exists a number
is called bounded above if there exists a number 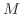 such that
such that
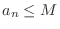 for all
for all  . A sequence
. A sequence  is called bounded below if there exists a number
is called bounded below if there exists a number 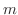 such that
such that
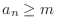 for all
for all  . Furthermore, a sequence
. Furthermore, a sequence  is called bounded if it is bounded above and bounded below..
is called bounded if it is bounded above and bounded below..
NOTE The sequence
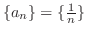 is bounded. For
is bounded. For
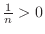 and
and
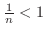 for all
for all  .
.
Monotonicity If
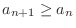 for all
for all  , a sequence
, a sequence  is called monotonically increasing. If
is called monotonically increasing. If
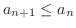 for all
for all  , a sequence
, a sequence  is called monotonicall decreasing sequence.
is called monotonicall decreasing sequence.
Strictly increasing As  gets larger, the value of
gets larger, the value of 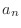 gets larger without equality. Then we say strictly increasing.
gets larger without equality. Then we say strictly increasing.
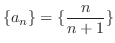 is monotonically increasings.
is monotonically increasings.
SOLUTION We use the ratio to check to see. Note that
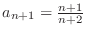 .
.
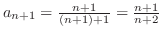 .
.
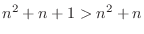 implies
implies
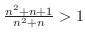 .
.
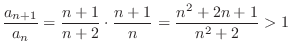
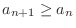 and
and  is monotonically increasing
is monotonically increasing

SOLUTION Since
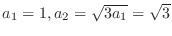 , we have
, we have
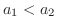 . Now use mathematical induction. Show the statement is true for
. Now use mathematical induction. Show the statement is true for 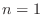 and assume true
and assume true 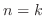 . If the statement is true for
. If the statement is true for 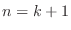 , then it is ture for all
, then it is ture for all  .
.
For 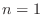 ,
,
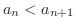 is true. Now assume that
is true. Now assume that
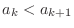 is true. Then we have
is true. Then we have
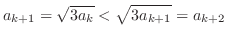
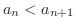 for all
for all 

Limit of sequence As  approaches
approaches 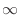 ,
, 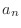 approaches
approaches 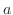 . Then we write
. Then we write
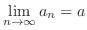
 converges to
converges to 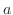 and call this
and call this 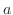 limit.
limit.
NOTE When a sequence converges to 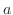 ,
, 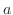 has to be a real number. Thus we can not use
has to be a real number. Thus we can not use 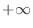 or
or 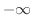 for
for 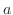 . When a sequence
. When a sequence  does not converge, we say
does not converge, we say  diverges.
diverges.
Understanding Limit We can think of
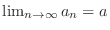 as the value of
as the value of
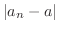 gets close to 0.
gets close to 0.
Types of divergence There are basically two types of divergence. As  gets larger,
gets larger, 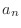 gets larger without bound. In this case, we write
gets larger without bound. In this case, we write
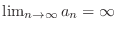 . As
. As  gets larger,
gets larger, 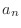 takes the postive value and negative value and never approaches any number. In this case, we say the sequence bibrates.
takes the postive value and negative value and never approaches any number. In this case, we say the sequence bibrates.
Limit properties
NOTE When the limit exits, four arithmetic operations hold. Express 1. by
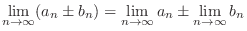
Limit properties
NOTE Suppose that the denominator of the sequence approaches some positive constant as the numerator approaches 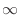 , Then the sequence gets larger without bound. Thus the sequence diverges. Suppose next that the denominator of the sequence approaches
, Then the sequence gets larger without bound. Thus the sequence diverges. Suppose next that the denominator of the sequence approaches 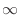 as the numerator approaches a positive constant. Then the limit of the sequence is 0.
as the numerator approaches a positive constant. Then the limit of the sequence is 0.
Indeterminate What happens if the numerator and the denominator approach 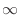 . In this case, we say indeterminate. If this happens, we factor by taking out the highest power of
. In this case, we say indeterminate. If this happens, we factor by taking out the highest power of  from the numerator and the denominato. Then apply theorem1.1.4.
from the numerator and the denominato. Then apply theorem1.1.4.
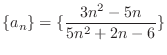
Basic limit
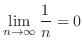
SOLUTION
As
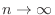 ,
,
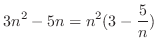
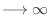 and
and
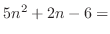
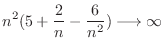 . Then we factor by taking out
. Then we factor by taking out 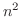 to have
to have
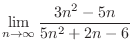 |
 |
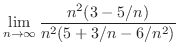 |
|
 |
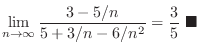 |
 |
 |
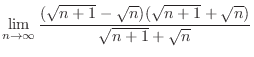 |
|
 |
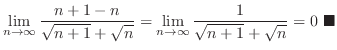 |
To find the limit, the theorem above is not enough. For example, consider
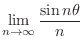 as
as
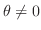 .
.
In this problem, we can not obtain the limit by using the theorem 1.1 and the theorem 1.2. To find the limit of
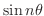 , it is useful to use the following theorem.
Squeezing theorem
, it is useful to use the following theorem.
Squeezing theorem
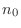 so that
so that
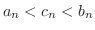 is true for all
is true for all 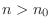 and
and
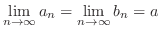
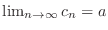 .
.
Absolute-value inequalities Subtract 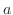 from the inequality
from the inequality
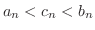 . Then
. Then
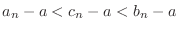 . If
. If
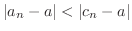 , then we have
, then we have
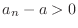 and
and
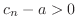 . Thus
. Thus
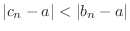 .
.
Proof. Since
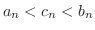 , we have either
, we have either
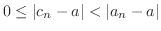 or
or
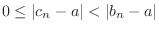 .
Note that
.
Note that
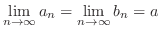
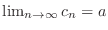

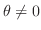 , find the limit of the following.
, find the limit of the following.
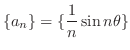
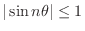 , we have
, we have
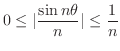
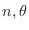 . Thus we can sandwich
. Thus we can sandwich
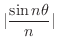 using 0 and
using 0 and
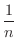 . Now taking the limit of 0 and
. Now taking the limit of 0 and
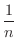 , we obtain
, we obtain
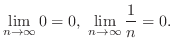
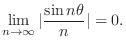
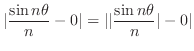
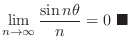
Property of
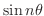 Since
Since
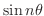 is a periodic and
is a periodic and
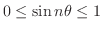 .
.
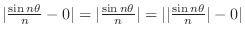
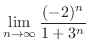 2.
2.
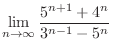
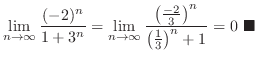
limit of 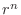
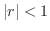 implies
implies
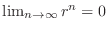
2.
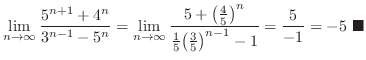
The limit of 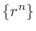 is the base of convergence and divergence.
is the base of convergence and divergence.
Bernoulli inequality
For 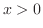 and
and 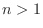 ,
,
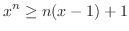
Proof
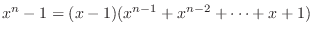 .
.
For 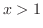 , we have
, we have 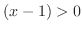 and
and
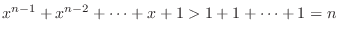
For 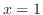 , we have
, we have 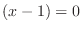 and
and
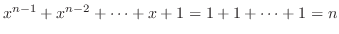
For 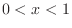 , we have
, we have 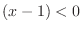 and
and
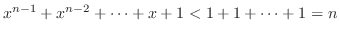 . Thus,
. Thus,
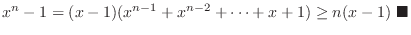
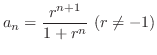 , find
, find
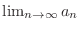 .
. 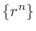 .
.
Bernoulli inequality By the Bernoulli inequality, 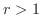 implies that
implies that
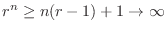 .
.
For 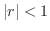 , we consider
, we consider
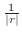 . Then
. Then
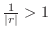 and
and
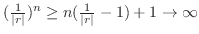 .
.
Thus, for 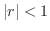 we have
we have 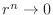 .
.
Divide the numerator and the denominator of
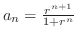 by
by 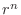 .
.
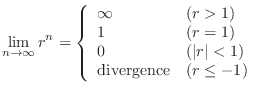
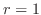 ,
,
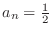 and
and
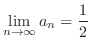 .
For
.
For 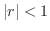 ,
,
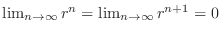 and
and
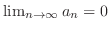 .
.
For
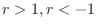 ,
,
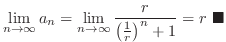
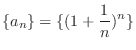 is monotonically increasing.
is monotonically increasing. 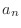 and
and 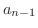 .
.
SOLUTION
Since
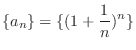 , we have
, we have
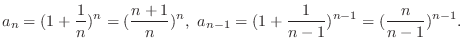
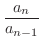 |
 |
![$\displaystyle (\frac{n+1}{n})^{n}(\frac{n-1}{n})^{n-1} = \frac{n}{n-1}[(\frac{n+1}{n})(\frac{n-1}{n})]^n$](img707.png) |
|
 |
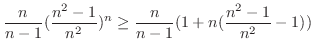 |
||
 |
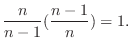 |
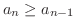 and
and  is monotonically increasing
is monotonically increasing

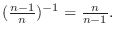 Bernoulli inequality
Bernoulli inequality
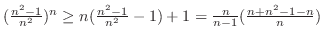
How to use MCT If you have no idea about the sequence converges or not, this theorem may help.
NOTE If a sequence  is monotonically increasing and bounded above, then there exists a number for which the sequence
is monotonically increasing and bounded above, then there exists a number for which the sequence  can not become greater than that number. Among all those numbers, we let the least number be
can not become greater than that number. Among all those numbers, we let the least number be 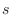 . Then the difference between
. Then the difference between 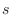 and
and 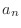 becomes small. Thus the sequence
becomes small. Thus the sequence  converges.
converges.
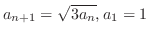 . Determine the sequence
. Determine the sequence  converges or diverges..
converges or diverges..  converges.
converges.
To show the sequence converges, it is enough to show the sequence  is bounded above increasing sequence or bounded below decreasing sequence.
is bounded above increasing sequence or bounded below decreasing sequence.
By Exercise1.14, we know  is monotonically increasing sequence. So, we need to show the sequence is bounded above. We use mathematical induction on
is monotonically increasing sequence. So, we need to show the sequence is bounded above. We use mathematical induction on  .
.
Since
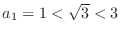 , it is true for
, it is true for  .
.
Assume that 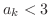 . Then
. Then
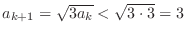 . Thus for all
. Thus for all  ,
, 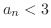 and
and  is bounded above increasing sequence. Therefore,
is bounded above increasing sequence. Therefore,  converges
converges

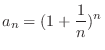 . Determine the sequence
. Determine the sequence  converges or diverges.
converges or diverges. 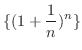 is monotonically increasing. Thus we need to show the sequence is bounded above.
is monotonically increasing. Thus we need to show the sequence is bounded above.
Expand
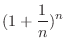
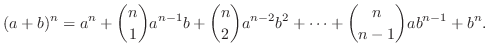
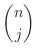 is called binomial coefficient.
using binomial theorem,
is called binomial coefficient.
using binomial theorem,
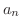 |
 |
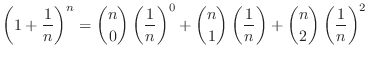 |
|
 |
 |
||
 |
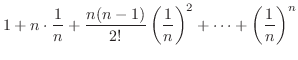 |
||
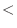 |
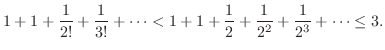 |
| Check |
|---|
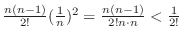
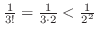
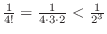
Thus, the sequence |
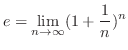
Eulre  The number
The number 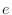 is defined by Swiss mathematitian Leonard Euler (1707-1783). The choice of
is defined by Swiss mathematitian Leonard Euler (1707-1783). The choice of 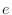 is from his name,
is from his name,
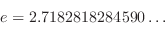 is known to be irrational.
is known to be irrational.
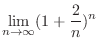
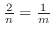 . Then
. Then
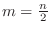 and
and
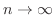 implies that
implies that
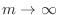 . Thus,
. Thus,
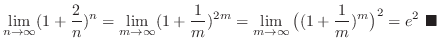
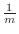 instead of
instead of
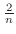 .
.
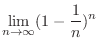
Express
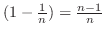 and use
and use
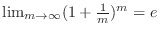 .
.
SOLUTION Since
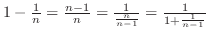 , we have
, we have
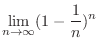 |
 |
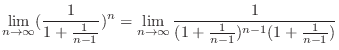 |
|
 |
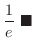 |
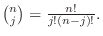
NOTE Since
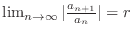 , for all
, for all  such that
such that 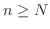 , we have
, we have
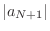 |
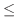 |
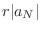 |
|
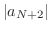 |
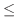 |
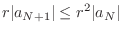 |
|
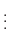 |
|||
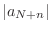 |
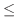 |
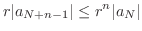 |
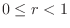 , we have
, we have
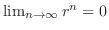 . Thus,
. Thus,
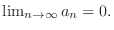
| Limit with absolute value |
|---|
 implies implies 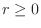 . .
|
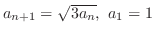
SOLUTION
Note that if  converges to
converges to 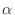 , then
, then
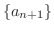 converges to
converges to 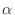 . Thus we have
. Thus we have
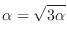
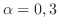 . Since
. Since 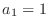 , it is impossible to have
, it is impossible to have
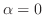 . So we have
. So we have
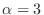 . Note this is not the end of proof. We have to show
. Note this is not the end of proof. We have to show
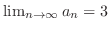 .
.
Let
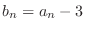 . If we can show
. If we can show
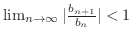 , then we can show
, then we can show
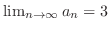 .
.
By the limit ratio test, it is enough to show
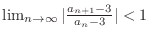 .
.
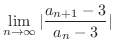 |
 |
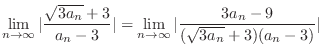 |
|
 |
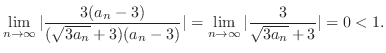 |
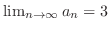

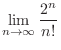
Limit of factorial To find the limit invloving factorials or power functions, it is useful to use the limit ration theorem.
| Check |
|---|
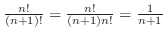 . .
|
SOLUTION Set
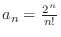 . Then
. Then
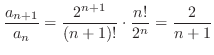
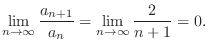
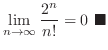
 of the following sequences:
of the following sequences:
![$\displaystyle{\lim_{n \rightarrow \infty}\sqrt[n]{a} = 1}$](img807.png) for
for 
![$\displaystyle{\lim_{n \rightarrow \infty}\sqrt[n]{a} = 1}$](img807.png) , find the limit of the followings:
, find the limit of the followings:
