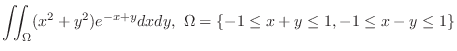Next: Improper Double Integrals Up: Multiple Integrals Previous: Repeated Integrals Contents Index
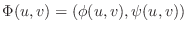 , the region
, the region 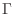 is mapped into
is mapped into  . Furthermore,
. Furthermore,
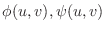 are the class
are the class 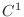 with respect to
with respect to 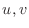 . Now suppose that Jacobian of
. Now suppose that Jacobian of 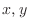 with respect to
with respect to 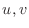
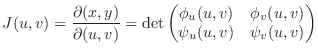
 . Then the following is true for the continuous function
. Then the following is true for the continuous function  on
on  .
.
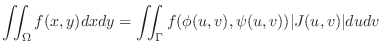
NOTE
Let  be the region on
be the region on 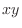 -plane and
-plane and 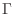 be the region on
be the region on 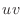 -plane. Suppose that
-plane. Suppose that 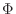 is a map from
is a map from 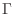 to
to  satisfying
satisfying
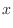 |
 |
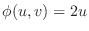 |
|
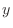 |
 |
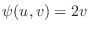 |
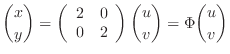
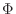 is invertible matrix. Thus there exists the inverse of
is invertible matrix. Thus there exists the inverse of 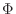 such that
such that
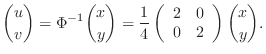
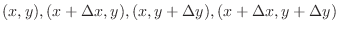 .
Then the area of the rectangle is
.
Then the area of the rectangle is
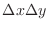 . Now correspondence area of
. Now correspondence area of  -plane is given by
-plane is given by
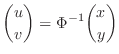
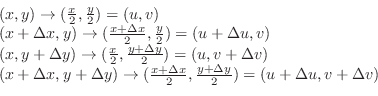
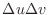 of
of 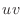 -plane is
-plane is
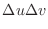 |
 |
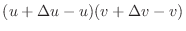 |
|
 |
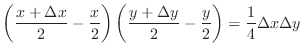 |
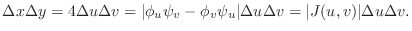
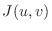 is the jacobian.
is the jacobian.
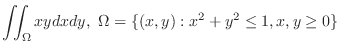
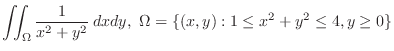
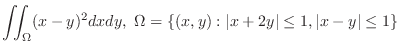
SOLUTION
1.  is a circular region. Thus using polar coordinate,
is a circular region. Thus using polar coordinate,
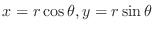 . Then
. Then
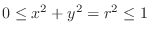 and
and
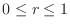 . Also,
. Also,
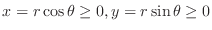 and
and
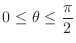 .
Thus
.
Thus  is transformed to
is transformed to
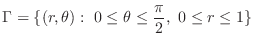
Then by Theorem5.5,
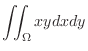 |
 |
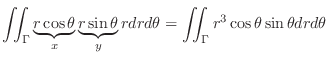 |
|
 |
![$\displaystyle \int_{0}^{\frac{\pi}{2}}\sin{\theta}\cos{\theta}d{\theta}\int_{0}...
...t \left[\frac{r^4}{4}\right ]_{0}^{1} = \frac{1}{8}
\ensuremath{ \blacksquare}$](img1239.png) |
 is a washer region. Then by letting
is a washer region. Then by letting
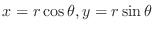 , we have
, we have
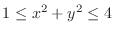 and
and
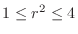 . Here since
. Here since 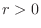 ,
,
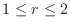 . Also since
. Also since
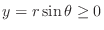 ,
,
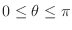 . Thus
. Thus  is transformed into
is transformed into
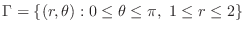
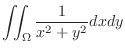 |
 |
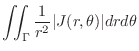 |
|
 |
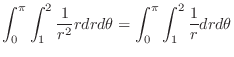 |
||
 |
![$\displaystyle \int_{0}^{\pi} d\theta [\log{r}]_{1}^{2} = \pi \log{2} \ensuremath{ \blacksquare}$](img1252.png) |
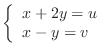 . Then solve for
. Then solve for 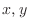 to get
to get
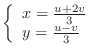 Substitute this into the condition of
Substitute this into the condition of  . Then the point of
. Then the point of
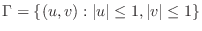 corresponds one-to-one into point in
corresponds one-to-one into point in  . Now
. Now
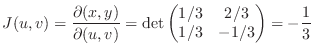
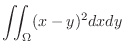 |
 |
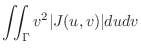 |
|
 |
![$\displaystyle \int_{-1}^1 du \int_{-1}^1 \frac{v^2}{3}dv = [u]_{-1}^{1}\left[\frac{v^3}{9}\right]_{-1}^{1}$](img1262.png) |
||
 |
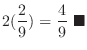 |
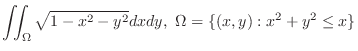
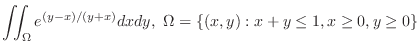
 is a circlular region . Thus use the polar coordinate
is a circlular region . Thus use the polar coordinate
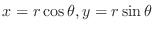 . Since
. Since
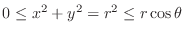 ,
,
 and
and
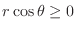 . Now
. Now
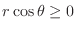 implies
implies
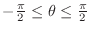 . Since
. Since
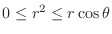 ,
,
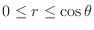 . Thus,
. Thus,  is transformed into
is transformed into
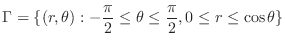
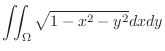 |
 |
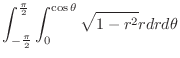 |
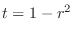 . Then
. Then
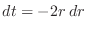 ,
,
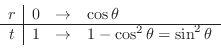 . Thus,
. Thus,
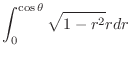 |
 |
![$\displaystyle -\frac{1}{2}\int_1^{\sin^{2}{\theta}}t^{\frac{1}{2}}\:dt = -\frac{1}{2}\cdot\frac{2}{3}\left[t^{3/2}\right]_1^{\sin^{2}{\theta}}$](img1279.png) |
|
 |
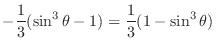 |
Thus,
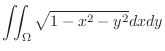 |
 |
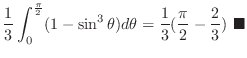 |
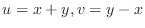 . Then check to see where the region
. Then check to see where the region
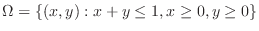 map into.
map into.
Since
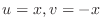 , the line , the line 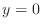 maps to maps to 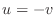 . . |
Since
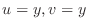 , the line , the line 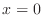 maps to maps to 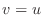 |
A line 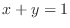 maps to maps to
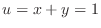 |
 is mapped to
is mapped to
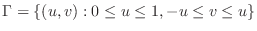
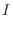 |
 |
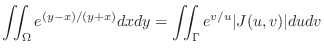 |
|
 |
![$\displaystyle \frac{1}{2}\int_{0}^{1}\int_{u}^{u}e^{v/u}dvdu = \frac{1}{2}\int_{0}^{1}[ue^{v/u}]_{-u}^{u} du$](img1300.png) |
||
 |
![$\displaystyle \frac{1}{2}\int_{0}^{1}(ue - ue^{-1})du = \frac{1}{2}[\frac{u^2 e...
...frac{u^2}{2e}]_{0}^{1} = \frac{1}{4}(e-\frac{1}{e}) \ensuremath{ \blacksquare}$](img1301.png) |
Exercise A
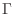 which is the image of
which is the image of
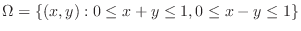 by the transformation
by the transformation
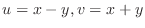 DThen using this transformation, evaluate
DThen using this transformation, evaluate
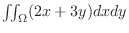 D
D
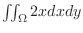 , where
, where
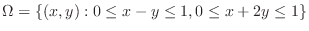 .
.
Exercise B
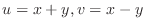 , evaluate the following double integral.
, evaluate the following double integral.