Repeated Integrals

**Figure 5.2:** Vertically Simple Region
$\includegraphics[width=4cm]{SOFTFIG-5/v-simple.eps}$

**Figure 5.3:** Horizontal simple
$\includegraphics[width=5cm]{SOFTFIG-5/h-simple.eps}$

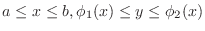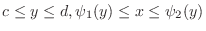The closed region $\Omega$ bounded by $a \leq x \leq b, \phi_{1}(x) \leq y \leq \phi_{2}(x)$ is called Vertically simple region, The closed region $\Omega$ bounded by $c \leq y \leq d, \psi_{1}(y) \leq x \leq \psi_{2}(y)$ is called Horizontally simple region.

Theorem 5..3 1. If $f(x,y)$

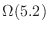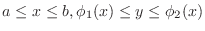is continuous on the closed region $% latex2html id marker 29390 $ \Omega(\ref{fig:V-simple})$$ bounded by $a \leq x \leq b, \phi_{1}(x) \leq y \leq \phi_{2}(x)$ , then

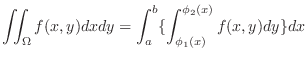
$\displaystyle \iint_{\Omega}f(x,y)dxdy = \int_{a}^{b}\{\int_{\phi_{1}(x)}^{\phi_{2}(x)}f(x,y)dy\}dx$

2. If

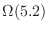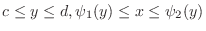is continuous on the closed region $% latex2html id marker 29398 $ \Omega(\ref{fig:V-simple})$$ bounded by $c \leq y \leq d, \psi_{1}(y) \leq x \leq \psi_{2}(y)$ , then

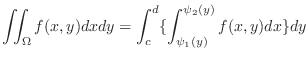
$\displaystyle \iint_{\Omega}f(x,y)dxdy = \int_{c}^{d}\{\int_{\psi_{1}(y)}^{\psi_{2}(y)}f(x,y)dx\}dy$

Example 5..2 Given the region $\Omega$ as in the figure 5.4, evaluate the following double integral

$\displaystyle \iint_{\Omega}(x^2 - y)dxdy$

**Figure 5.4:** $-x^2 \leq y \leq x^2$
$% latex2html id marker 29412 \includegraphics[width=4.5cm]{SOFTFIG-5/reidai5-2.eps}$

SOLUTION When a horizontal line is drawed to the region $\Omega$ , it intersects the curve more than once. But when a vertical line is drawed to the region $\Omega$ , it does not intersect more than once. Thus the region is vertically simple region. Now fix $x$

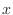. Then the region is in between the curve $y = -x^2$

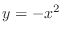and the curve $y = x^2$

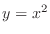. Thus we have 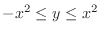$-x^2 \leq y \leq x^2$ . Next free $x$

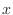to get 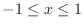$-1 \leq x \leq 1$ . Thus $\Omega$ is expressed as follows.

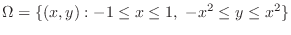
$\displaystyle \Omega = \{(x,y) : -1 \leq x \leq 1, -x^2 \leq y \leq x^2 \}$

Therefore,

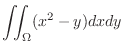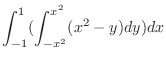$\displaystyle \iint_{\Omega}(x^2 - y)dxdy$	$\displaystyle =$	$\displaystyle \int_{-1}^{1}(\int_{-x^2}^{x^2}(x^2 - y)dy)dx$
	$\displaystyle =$	$\displaystyle \int_{-1}^{1}\left[(x^2 y - \frac{1}{2}y^2) \right ]_{-x^2}^{x^2} dx$
	$\displaystyle =$	$\displaystyle \int_{-1}^{1}[(x^4 - \frac{1}{2}x^4) - (-x^4 - \frac{1}{2}x^4)]dx$
	$\displaystyle =$	$\displaystyle \int_{-1}^{1}2x^4dx = \left[\frac{2}{5}x^5 \right ]_{-1}^{1} = \frac{4}{5} \ensuremath{ \blacksquare}$

Exercise 5..2 Give the region $\Omega$ as in the figure 5.5, evaluate the following double integral.

$\displaystyle \iint_{\Omega}(x^{1/2} - y^2)dxdy$

**Figure 5.5:** $x^2 \leq y \leq x^{1/4}$
$% latex2html id marker 29469 \includegraphics[width=5.5cm]{SOFTFIG-5/enshu5-2.eps}$

SOLUTION This region is both vertically simple region and horizontally simple region. We first evaluate the integral by using vertically simple region.

$\Omega$ can be expressed by the following.

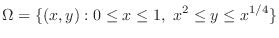
$\displaystyle \Omega = \{(x,y) : 0 \leq x \leq 1, x^2 \leq y \leq x^{1/4} \}$

Thus

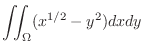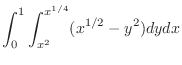$\displaystyle \iint_{\Omega}(x^{1/2} - y^2)dxdy$	$\displaystyle =$	$\displaystyle \int_{0}^{1}\int_{x^2}^{x^{1/4}}(x^{1/2} - y^2)dydx$
	$\displaystyle =$	$\displaystyle \int_{0}^{1}\left[x^{1/2}y - \frac{1}{3}y^3\right ]_{x^2}^{x^{1/4}}dx$
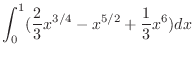	$\displaystyle =$	$\displaystyle \int_{0}^{1}(\frac{2}{3}x^{3/4} - x^{5/2} + \frac{1}{3}x^{6})dx$
	$\displaystyle =$	$\displaystyle \left[\frac{8}{21}x^{7/4} - \frac{2}{7}x^{7/2} + \frac{1}{21}x^7\right ]_{0}^{1}$
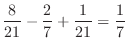	$\displaystyle =$	$\displaystyle \frac{8}{21} - \frac{2}{7} + \frac{1}{21} = \frac{1}{7}$

This time, we evaluate the integral by using horizontally simple region. $\Omega$ can be expressed by the following.

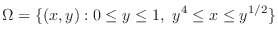
$\displaystyle \Omega = \{(x,y) : 0 \leq y \leq 1, y^4 \leq x \leq y^{1/2} \}$

Then

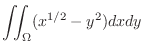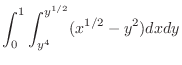$\displaystyle \iint_{\Omega}(x^{1/2} - y^2)dxdy$	$\displaystyle =$	$\displaystyle \int_{0}^{1}\int_{y^4}^{y^{1/2}}(x^{1/2} - y^2)dxdy$
	$\displaystyle =$	$\displaystyle \int_{0}^{1}\left[\frac{2}{3}x^{3/2} - y^2 x\right ]_{y^4}^{y^{1/2}}dy$
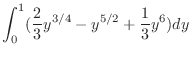	$\displaystyle =$	$\displaystyle \int_{0}^{1}(\frac{2}{3}y^{3/4} - y^{5/2} + \frac{1}{3}y^{6})dy$
	$\displaystyle =$	$\displaystyle \left[\frac{8}{21}y^{7/4} - \frac{2}{7}y^{7/2} + \frac{1}{21}y^7\right ]_{0}^{1}$
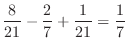	$\displaystyle =$	$\displaystyle \frac{8}{21} - \frac{2}{7} + \frac{1}{21} = \frac{1}{7}$

We obtain the same result as expected $\blacksquare$

Interchage from vertically simple region to horizontally simple region or vice versa. Then corresponding integral change the order of integration.

Example 5..3 Evaluate the following double integral.

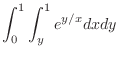
$\displaystyle \int_{0}^{1}\int_{y}^{1}e^{y/x}dxdy$

SOLUTION We can not evaluate the integral 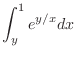$\displaystyle{\int_{y}^{1}e^{y/x} dx}$ . Then by the change the order of integration, the region $\Omega$ is given by

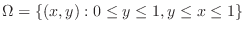
$\displaystyle \Omega = \{(x,y) : 0 \leq y \leq 1, y \leq x \leq 1\}$

Thus it is given by the horizontally simple region. Now express $\Omega$ by the vertically simple region.

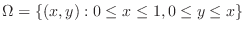
$\displaystyle \Omega = \{(x,y) : 0 \leq x \leq 1, 0 \leq y \leq x\}$

Then

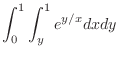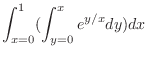$\displaystyle \int_{0}^{1}\int_{y}^{1}e^{y/x}dxdy$	$\displaystyle =$	$\displaystyle \int_{x=0}^{1}(\int_{y=0}^{x}e^{y/x}dy) dx$
	$\displaystyle =$	$\displaystyle \int_{0}^{1}[xe^{y/x}]_{0}^{x} dx$
	$\displaystyle =$	$\displaystyle \int_{0}^{1}(xe - x)dx = \left[\frac{(e-1)x^2}{2}\right]_{0}^{1} = \frac{e-1}{2}\ensuremath{ \blacksquare}$

Exercise 5..3 Evaluate the following double integral.

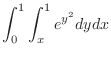
$\displaystyle \int_{0}^{1}\int_{x}^{1}e^{y^2}dydx$

SOLUTION Note that 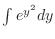$\int e^{y^2}dy$ is known for non-integrable. Thus it is impossible to integrate 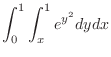$\displaystyle{\int_{0}^{1}\int_{x}^{1}e^{y^{2}} dy dx}$ in this order. Thus, interchange the order of integration. Since

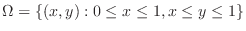
$\displaystyle \Omega = \{(x,y) : 0 \leq x \leq 1, x \leq y \leq 1\}$

is given by the vertically simple region. Then express $\Omega$ by the horizontally simple region.

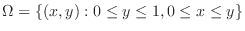
$\displaystyle \Omega = \{(x,y) : 0 \leq y \leq 1, 0 \leq x \leq y\}$

Thus,

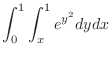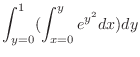$\displaystyle \int_{0}^{1}\int_{x}^{1}e^{y^{2}} dy dx$	$\displaystyle =$	$\displaystyle \int_{y=0}^{1}(\int_{x=0}^{y}e^{y^{2}}dx) dy$
	$\displaystyle =$	$\displaystyle \int_{0}^{1}[xe^{y^{2}}]_{0}^{y} dy$
	$\displaystyle =$	$\displaystyle \int_{0}^{1}ye^{y^{2}} dy = \left[\frac{1}{2}e^{y^2}\right]_{0}^{1} = \frac{e-1}{2}\ensuremath{ \blacksquare}$

Exercise A

1.

Evaluate the following double integrals．

(a) $\displaystyle{\iint_{\Omega}x dxdy, \Omega: -1 \leq x \leq 1, 0 \leq y \leq 3}$

(b) $\displaystyle{\iint_{\Omega}(2x + 3y) dxdy, \Omega: 0 \leq x \leq 1, 0 \leq y \leq x}$

(d) $\displaystyle{\iint_{\Omega}\sin(x+y) dxdy, \Omega: 0 \leq x \leq \frac{\pi}{2}, 0 \leq y \leq \frac{\pi}{2}}$

(e) $\displaystyle{\iint_{\Omega}x^{3} y dxdy, \Omega: 0 \leq x \leq 1, 0 \leq y \leq x}$

2.

Interchange the order of integration．

(a) $\displaystyle{\int_{0}^{1}\int_{x^{2}}^{x}f(x,y)dydx}$ (b) $\displaystyle{\int_{0}^{1}\int_{0}^{y^{2}}f(x,y)dxdy}$ (c) $\displaystyle{\int_{0}^{2}\int_{\frac{x}{2}}^{3-x}f(x,y)dydx}$

3.

Answer the following questions．

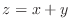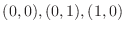
(a) Find the volume of solid bounded by the following surface under the surface $z = x+y$ and above the triqngle $(0,0), (0,1), (1,0)$

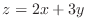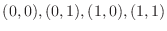(b) Find the volume of solid bounded by the following surface under the surface $z = 2x+3y$ and qbove the square $(0,0), (0,1), (1,0), (1,1)$ .

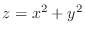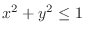
(c) Find the volume of the solid bounded above by the surface $z = x^{2} + y^{2}$ and below by the plane $x^{2} + y^{2} \leq 1$

Exercise B

1.

Evaluate the following double integrals．

(a) $\displaystyle{\iint_{\Omega}x^2 dxdy, \Omega: -1 \leq x \leq 1, 0 \leq y \leq 3}$

(b) $\displaystyle{\iint_{\Omega}e^{x+y} dxdy, \Omega: 0 \leq x \leq 1, 0 \leq y \leq x}$

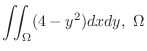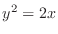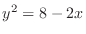(d) $\displaystyle{\iint_{\Omega}(4 - y^2) dxdy, \Omega}$ is bounded by $y^2 = 2x$ and $y^2 = 8 - 2x$ .

2.

Interchange the order of integrals.

(a) $\displaystyle{\int_{0}^{1}\int_{x^4}^{x^2}f(x,y)dydx}$ (b) $\displaystyle{\int_{0}^{1}\int_{-y}^{y}f(x,y)dxdy}$ (c) $\displaystyle{\int_{1}^{4}\int_{x}^{2x}f(x,y)dydx}$

3.

Evaluate the following double integrals．

(a) $\displaystyle{\int_{0}^{1}\int_{y}^{1}e^{y/x}dxdy}$ (b) $\displaystyle{\int_{0}^{1}\int_{x}^{1}e^{y^2}dydx}$ (c) $\displaystyle{\int_{0}^{1} dy \int_{y}^{\sqrt{y}}\frac{\sin{x}}{x}dx}$