Next: Application of Double Integrals Up: Multiple Integrals Previous: Change of Variables Contents Index
The double integrals treated so far are the case where a function is bounded on the bounded region. Now consider the case where  is not bounded.
is not bounded.
The sequence of bounded closed regions
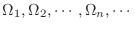 in
in  satisfy
satisfy
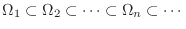
 is a subset of
is a subset of
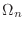 .
Then if
.
Then if  is integrable on the region
is integrable on the region
 ,
,
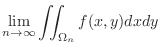
 is integrable on
is integrable on  and define
and define
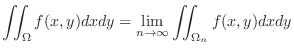
SOLUTION
1. Using horizontally simple region, we have
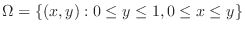 . Then
. Then
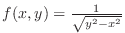 is discontinuous at
is discontinuous at 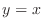 . Thus let
. Thus let
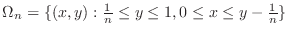 . Then
. Then
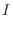 |
 |
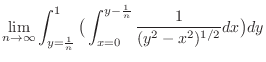 |
|
 |
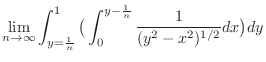 |
||
 |
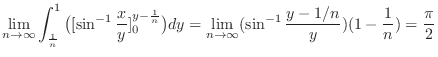 |
2. The region  is not bounded. So, consider the sequence of closed bounded regions
is not bounded. So, consider the sequence of closed bounded regions
 .
.
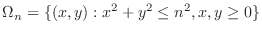
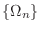 is given by the figure 5.7.
For
is given by the figure 5.7.
For
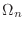 , use the polar coordinate
, use the polar coordinate
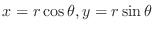
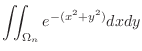 |
 |
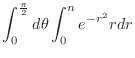 |
|
 |
![$\displaystyle \frac{\pi}{2}\left[-\frac{e^{-r^2}}{2}\right ]_{0}^{n} = \frac{\pi}{4}(1 - e^{-n^2})$](img1346.png) |
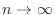 , we find
, we find
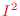 and
and
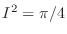
 Consider a function
Consider a function  is not bounded on
is not bounded on  .
.
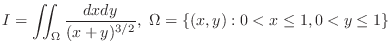
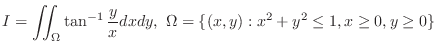
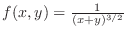 is discontinuous at
is discontinuous at  . Then create
. Then create 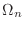 so that
so that  is not included in
is not included in 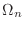 .
.
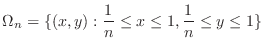
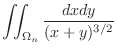 |
 |
![$\displaystyle \int_{1/n}^{1}dx\int_{1/n}^{1} \frac{dy}{(x+y)^{3/2}} = \int_{1/n}^{1}\left[-\frac{2}{(x+y)^{1/2}}\right ]_{\frac{1}{n}}^{1}dx$](img1362.png) |
|
 |
![$\displaystyle 2\int_{1/n}^{1}[(x+\frac{1}{n})^{-\frac{1}{2}} - (x+1)^{-\frac{1}{2}} ]dx$](img1363.png) |
||
 |
![$\displaystyle 2\left[2(x+\frac{1}{n})^{\frac{1}{2}} - 2(x+1)^{\frac{1}{2}}\right ]_{\frac{1}{n}}^{1}$](img1364.png) |
||
 |
![$\displaystyle 4[2(1+\frac{1}{n})^{\frac{1}{2}} - \sqrt{2} - (\frac{2}{n})^{\frac{1}{2}}]$](img1365.png) |
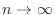 we can find
we can find
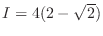

2.
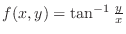 is bounded except on
is bounded except on 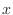 -axis.
-axis.
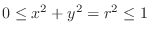 ,
,
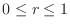 . Since
. Since
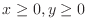 ,
,
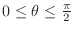 . Thus
. Thus  maps to
maps to
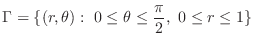
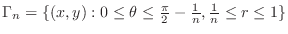 . Then,
. Then,
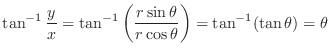
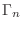 . Thus,
. Thus,
 |
 |
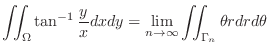 |
|
 |
![$\displaystyle \lim_{n \to \infty}\int_{\theta = 0}^{\frac{\pi}{2}-\frac{1}{n}}\...
...{\frac{\pi}{2}-\frac{1}{n}}\big(\left[\frac{r^2}{2}\right]_{\frac{1}{n}}^1\big)$](img1381.png) |
||
 |
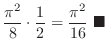 |
Exercise A
Exercise B
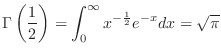 D
D