Next: Taylor Theorem for Two Up: Partial Differentiation Previous: Higher Order Partial Derivatives Contents Index
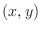 in the
in the 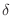 neighborhood of
neighborhood of 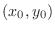 4.1
4.1
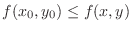 , then
, then 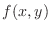 takes minimum at
takes minimum at
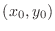 and
and
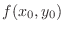 is called local minimum of
is called local minimum of 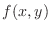 .
.
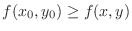 , then
, then 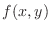 takes maximum at
takes maximum at
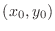 and
and
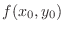 is called local maximum of
is called local maximum of 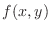 .
. NOTE A locam minimum and a local maximum togrther are called extrema.
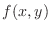 has a extremum at
has a extremum at
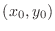 , then .
, then .
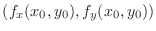 exists and
exists and
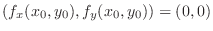 , or
, or
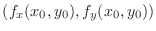 does not exist.
does not exist.
Proof
Since
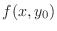 takes a extreme value at
takes a extreme value at 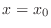 ,
,
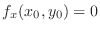 or
or
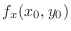 does not exist. Similarly for
does not exist. Similarly for 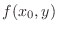 .
.
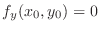 or
or
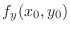 does not exist
does not exist

SOLUTION If
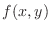 takes the extreme value at
takes the extreme value at
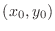 , then
, then
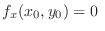 implies
implies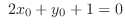
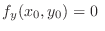 implies
implies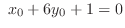
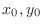 . Then
. Then
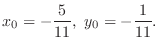
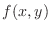 may takes the extreme value at
may takes the extreme value at
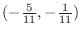 . Now we have to check to see if this is a local maximum or minimum.owari
. Now we have to check to see if this is a local maximum or minimum.owari
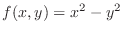
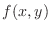 takes the extreme value at
takes the extreme value at
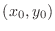 , then
, then
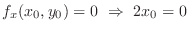
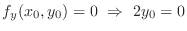
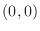 is a critical point. Now as
is a critical point. Now as 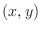 approaches
approaches 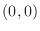 along
along 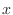 -axis, we have
-axis, we have
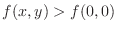 , along
, along 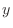 -axis we have
-axis we have
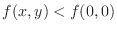 . Thus
. Thus 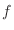 does not take the extreme value at
does not take the extreme value at 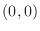

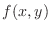 be the class
be the class 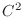 at
at 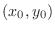 in the region
in the region 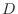 . If
. If
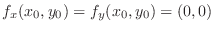 , then denote
, then denote
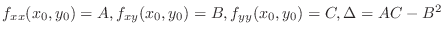 .
.
1. If
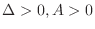 , then
, then
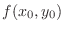 is a local minimum.
is a local minimum.
2. If
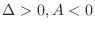 , then
, then
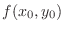 is a local maximum.
is a local maximum.
3. If
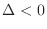 , then
, then
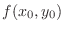 is a saddle point
is a saddle point
4. If
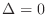 , then test is no conclusive.
, then test is no conclusive.