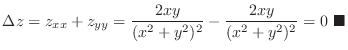Next: Extreme Values of Function Up: Partial Differentiation Previous: Partial Differentiation of Composite Contents Index
Suppose that partial derivatives
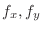 are again partially differentiable with respect to
are again partially differentiable with respect to 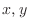 . Then
. Then
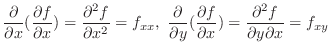
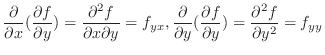
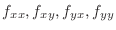 The second partial derivatives of
The second partial derivatives of 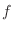 .
.
If  is the class
is the class 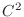 on
on 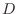 , then
, then
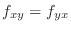 .
.
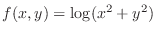 .
.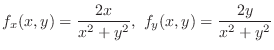 ,
,
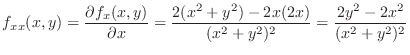 ,
,
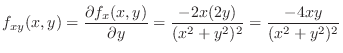 ,
,
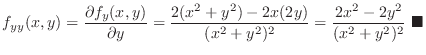
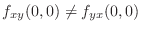 for the following function.
for the following function.
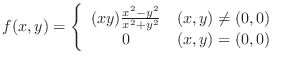
SOLUTION To show
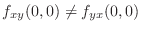 , we first evaluate these values.
, we first evaluate these values.
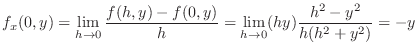
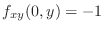 and
and
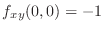 .
Next
.
Next
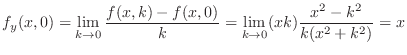
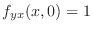 and
and
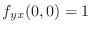 .
.
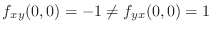

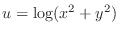 , show
, show
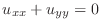 .
.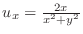 .
.
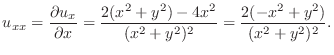
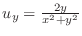 . Then
. Then
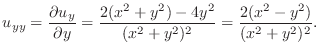
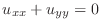

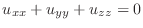
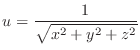
SOLUTION
Let
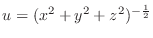 . Then
. Then
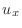 |
 |
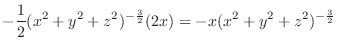 |
|
 |
 |
 |
|
 |
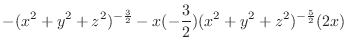 |
||
 |
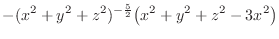 |
||
 |
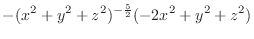 |
||
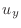 |
 |
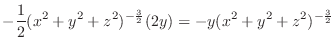 |
|
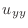 |
 |
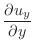 |
|
 |
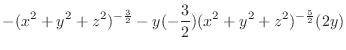 |
||
 |
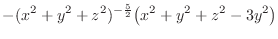 |
||
 |
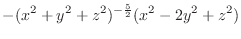 |
||
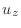 |
 |
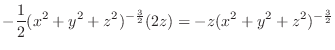 |
|
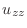 |
 |
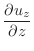 |
|
 |
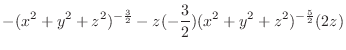 |
||
 |
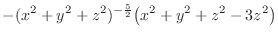 |
||
 |
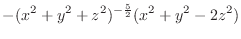 |
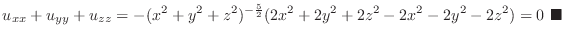
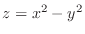 2.
2.
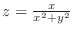
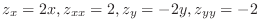 . Thus,
. Thus,
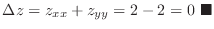 2.
2. 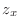 |
 |
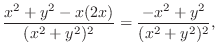 |
|
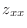 |
 |
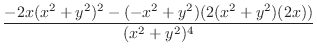 |
|
 |
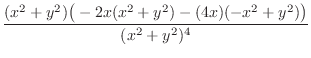 |
||
 |
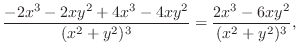 |
||
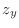 |
 |
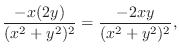 |
|
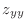 |
 |
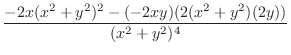 |
|
 |
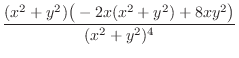 |
||
 |
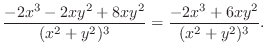 |
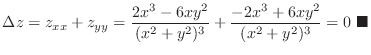
When we express
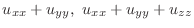 by
by 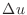 . Then
. Then 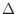 is called Laplaian and the class
is called Laplaian and the class 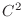 function
function 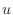 satisfying the equation
satisfying the equation
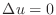 is called harmonic function.
is called harmonic function.

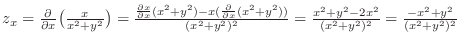
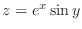 2.
2.
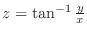
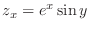 ,
,
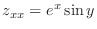 ,
,
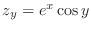 ,
,
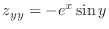 .
.
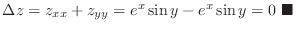
2.
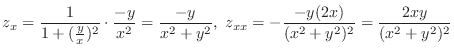
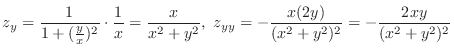 .
Thus,
.
Thus,