Next: Conditional Extrema Up: Extreme Values of Function Previous: Extreme Values of Function Contents Index
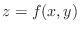 by a quadratic polynomial of
by a quadratic polynomial of 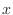 and
and 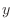 .
Let
.
Let
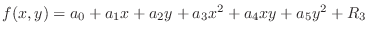 , where
, where 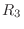 is an error term. Then find all 2nd order partial derivatives of
is an error term. Then find all 2nd order partial derivatives of
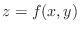 . If
. If 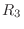 is so small that we can neglect, then
is so small that we can neglect, then
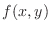 |
 |
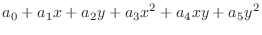 |
|
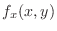 |
 |
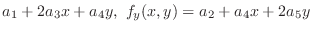 |
|
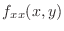 |
 |
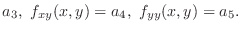 |
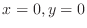 . Then
. Then
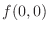 |
 |
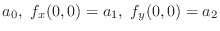 |
|
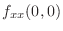 |
 |
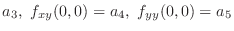 |
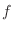 by the 2nd order partial derivatives. Therefore,
by the 2nd order partial derivatives. Therefore,
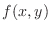 |
 |
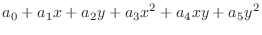 |
|
 |
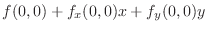 |
||
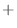 |
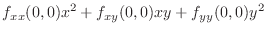 |
NOTE Let
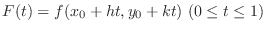 . Then
. Then 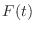 is the class
is the class 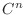 in
in 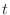 . Thus by Maclausin theorem,
. Thus by Maclausin theorem,
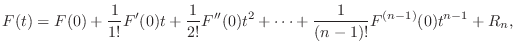
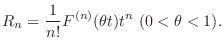
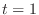 ,
,
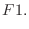 |
 |
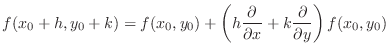 |
|
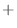 |
 |
||
 |
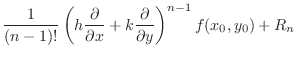 |
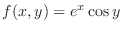 . Find the Taylor polynomial of 2nd degree at
. Find the Taylor polynomial of 2nd degree at  .
.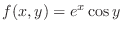 .
.
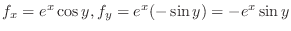 ,
,
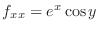 ,
,
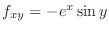 ,
,
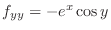 . Theorem4.7, let
. Theorem4.7, let
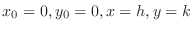 . Then
. Then
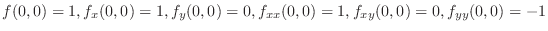 . Thus
. Thus
 |
 |
 |
|
 |
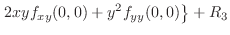 |
||
 |
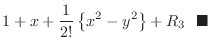 |
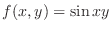 at
at
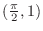 .
.
SOLUTION
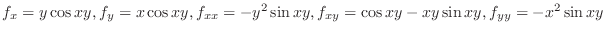 . Thus in Theorem4.7, let
. Thus in Theorem4.7, let
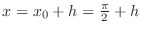 ,
,
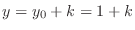 . Then
. Then
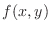 |
 |
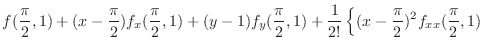 |
|
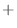 |
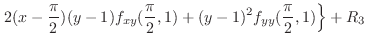 |
||
 |
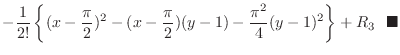 |
Proof
By Taylor theorem, for
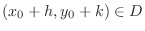 ,
we have
,
we have
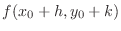 |
 |
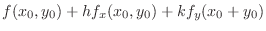 |
|
 |
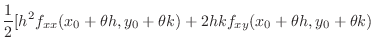 |
||
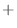 |
![$\displaystyle k^2 f_{yy} (x_{0}+\theta h,y_{0}+\theta k)], (0 < \theta < 1)$](img736.png) |
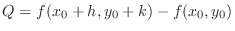 . Then
. Then
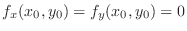 and
and
![$\displaystyle Q = \frac{1}{2}[h^2 f_{xx}(x_{0}+\theta h,y_{0}+\theta k) + 2hkf_...
...x_{0}+\theta h,y_{0}+\theta k) + k^2 f_{yy} (x_{0}+\theta h,y_{0}+\theta k) ]. $](img739.png)
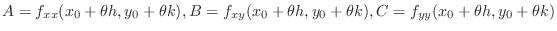 . Then
. Then
![$\displaystyle Q = \frac{1}{2}\left(Ah^2 + 2Bhk + Ck^2\right) = \frac{A}{2}\left[(h + \frac{Bk}{A})^2 + \frac{(AC - B^2)k^2}{A^2}\right]. $](img741.png)
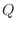 is determinde by the sign of
is determinde by the sign of 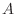 and the sign of
and the sign of 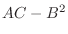 .
.
1. If
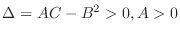 , then since
, then since  is the class
is the class 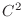 function, for any
function, for any 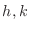 such that
such that 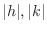 is sufficiently small and never 0 simulteneously, we have
is sufficiently small and never 0 simulteneously, we have 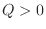 . Thus,
. Thus,
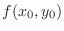 is a local minimum.
2. If
is a local minimum.
2. If
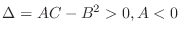 , then since
, then since  is the class
is the class 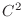 func, for any
func, for any 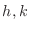 such that
such that 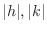 is sufficiently small and never 0 simulteneously, we have
is sufficiently small and never 0 simulteneously, we have 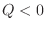 . Thus
. Thus
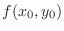 is a local maximum.
is a local maximum.
3. If
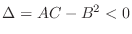 and
and 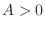 , then
, then 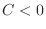 which gives a saddle point. Similarly, if
which gives a saddle point. Similarly, if
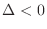 and
and 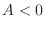 , then
, then 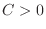 which give a saddle point.
which give a saddle point.

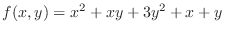
SOLUTION In Example4.16, we found the critical point. Now we check to see whether the function takes a local extremum at the critical point. Now by the 2nd derivative test,
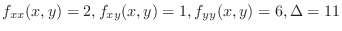
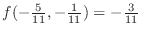 is a local minimum.
is a local minimum.

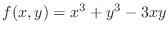
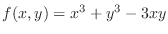 . Then we have
. Then we have
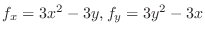 .
If
.
If  takes the local maxima at
takes the local maxima at
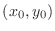 , then
, then
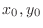 . Then substitute the equation
. Then substitute the equation
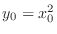 , which is derived from the equation 4.1, to the equation 4.2. Then
, which is derived from the equation 4.1, to the equation 4.2. Then
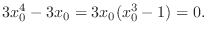
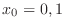 . Hence,
. Hence,
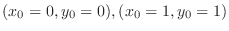 .
.
Now we apply the 2nd derivative test.
Since
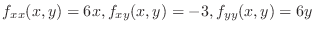 , at
, at  we have
we have
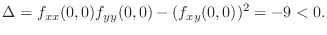
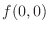 is not extrema.
Now at
is not extrema.
Now at 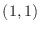 , we have
, we have
 |
 |
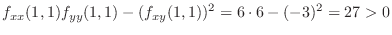 |
|
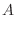 |
 |
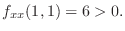 |
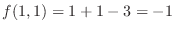 is the local minimum
is the local minimum

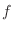 at
at 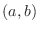 .D
.D
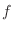 at
at 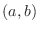 D
D