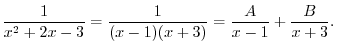Suppose that  is defined on is defined on ![$[a,b]$](img1084.png) . Partition the interval . Partition the interval ![$[a,b]$](img1084.png) into into  smaller intervals. Let smaller intervals. Let 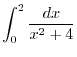 be such that for be such that for
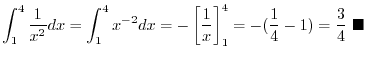
Figure 3.1:
Definite Integral
|
|
Express this partition by 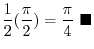 . The norm of the interval is the width of intervals that is . The norm of the interval is the width of intervals that is
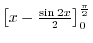 and denoted by and denoted by 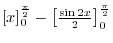 . Now take . Now take 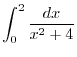 in the subinterval in the subinterval
![$[x_{i-1},x_{i}]$](img2920.png) and consider the sum called Riemann Sum and consider the sum called Riemann Sum
exists. Then we call  definite integral of definite integral of  and and  is called Riemann integrable function on is called Riemann integrable function on ![$[a,b]$](img1084.png) . We write . We write 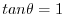 as as
|
![$[a,b]$](img1084.png) into
into 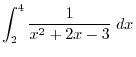 equal parts. Then
equal parts. Then
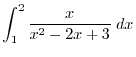 and
and