Next: Definite Integrals Up: Integration Previous: Integration of Trigonometric Functions Contents Index
1.
[2]
Integration of Irrational Functions Suppose that 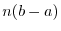 is a rational function of
is a rational function of 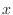 and
and 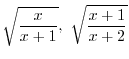 . Then
. Then
![$\displaystyle{\int R(x,\sqrt[n]{\rm linear\ polynomial })dx}$](img2838.png)
Let
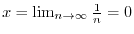 . Then we can get integration of rational function.
. Then we can get integration of rational function.
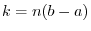
1. 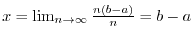 after completing the square. Then let
after completing the square. Then let
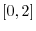
2. 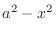 after completing the square. Then let
after completing the square. Then let
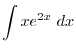
3.  after completing the square, Then let
after completing the square, Then let
 2.
2.
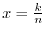 . Then
. Then 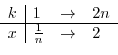 and
and
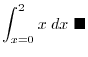 . Thus
. Thus
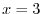 |
 |
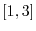 |
|
 |
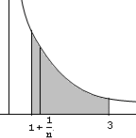 |
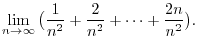 . Let
. Let
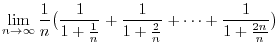 . Then
. Then
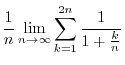 . Note that
. Note that
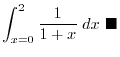 . Thus
. Thus
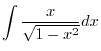 |
 |
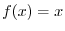 |
|
 |
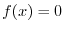 |
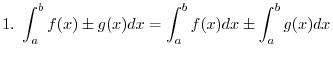 2.
2.
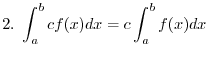
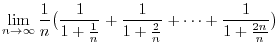 . Then
. Then
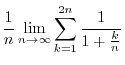 ,
,
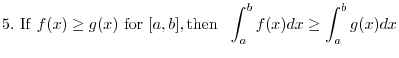 . Thus,
. Thus,
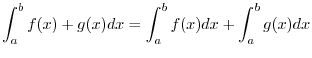 |
 |
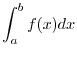 |
|
 |
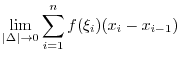 |
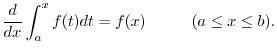
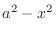 . Thus conside the right triangle with the hypotenuse
. Thus conside the right triangle with the hypotenuse 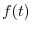 , the opposite side of the angle
, the opposite side of the angle 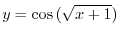 is
is 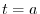 .
.
Let
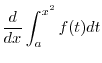 .
.
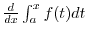 .
.
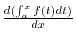
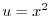

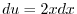

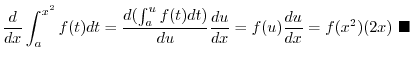

![$\displaystyle -\int{\frac{1 + \cos{2t}}{2}}\ dt = -[\frac{t}{2} + \frac{\sin{2t}}{4}] + c$](img2888.png)

![$\displaystyle -[\frac{t}{2} + \frac{\sin{t}\cos{t}}{2}] + c$](img2889.png)

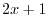
|
Exercise A
|
|
Exercise B
|