Next: Improper Integral Up: Integration Previous: Definite Integrals Contents Index
| u-substitution |
|---|
|
Theorem 3..11 If
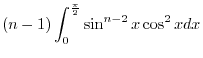 is differentiable on the open interval is differentiable on the open interval ![$[a,b]$](img1084.png) and and  is continuous on the closed interval is continuous on the closed interval
![$[\phi(a), \phi(b)]$](img3085.png) , then , then
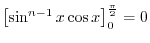
|
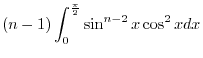 . Then
. Then
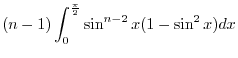 . Now the limit of intervals must be changed from
. Now the limit of intervals must be changed from
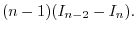 to
to 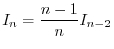 and
and
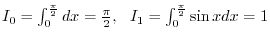 to
to 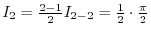 .
.
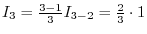 .
.
Integration by Parts
Let
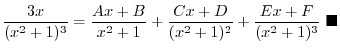 be differentiable on the closed interval
be differentiable on the closed interval ![$[a,b]$](img1084.png) . Then
. Then
![$\displaystyle \int_{a}^{b} f(x)g'(x) = \left[f(x)g(x)\right]_{a}^{b} - \int_{a}^{b} f'(x)g(x)dx $](img3093.png)
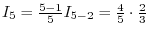 2.
2.
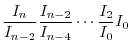
SOLUTION 1. Let
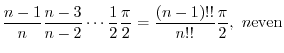 . Then
. Then
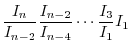 . Thus we can express the integrand as
. Thus we can express the integrand as 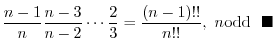 . Furthermore, the limit of integration becomes
. Furthermore, the limit of integration becomes
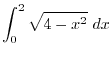 .
.
Thus,
![$\displaystyle{\int_{0}^{1}3x^{2}(x^{3}+1)^{4}dx = \int_{1}^{2}t^4 dt = \left[\f...
... \right ]_{1}^{2} = \frac{32 - 1}{5} = \frac{31}{5}}\ensuremath{\ \blacksquare}$](img3100.png)
2.
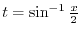 Then
Then
![$\displaystyle \int_{0}^{1}xe^x dx = [xe^x]_{0}^{1} - \int_{0}^{1}e^x dx = e - [e^x]_{0}^{1} = e - (e - 1) = 1.$](img3102.png)
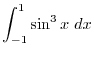
SOLUTION Let
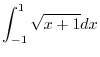 . Then,
. Then,
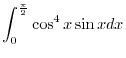 and
and
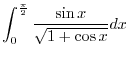 .
.
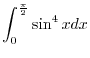 . Now need to express
. Now need to express 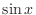 by
by 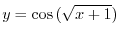 .
.
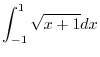 ,
,
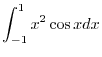 . Thus,
. Thus,
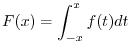
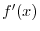 ,
,
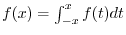 .
.
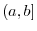 . Thus,
. Thus,
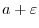
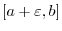
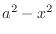 ,
,
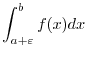 ,
,
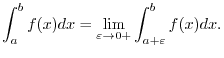 ,
,
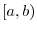 .
Since the limit of integral is
.
Since the limit of integral is
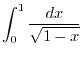 ,
,
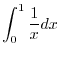
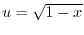 ,
,
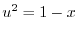 |
 |
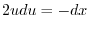 |
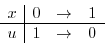 . Then
. Then
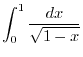 ,
,
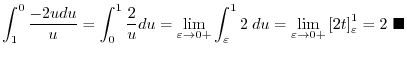 . Thus,
. Thus,
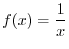 |
 |
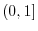 |
|
 |
![$\displaystyle \frac{\sqrt{2}}{2}\left[\log\vert\frac{1+u}{1-u}\vert\right]_{0}^...
...1 + \frac{\sqrt{2}}{2}}{1 - \frac{\sqrt{2}}{2}}\vert\ensuremath{\ \blacksquare}$](img3140.png) |
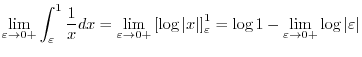
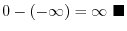 |
 |
 |
|
 |
 |
||
 |
![$\displaystyle \frac{\sqrt{2}}{2}\left[\log\vert\frac{1+t}{1-t}\vert\right]_0^{\...
...1 + \frac{\sqrt{2}}{2}}{1 - \frac{\sqrt{2}}{2}}\vert\ensuremath{\ \blacksquare}$](img3146.png) |
2. If
3.
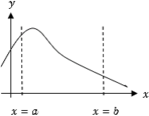
Properties of Definite Integral Suppose that  is continuous on the limit of integration.
is continuous on the limit of integration.
1. If  is even function, then
is even function, then
 is odd function, then
is odd function, then
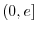
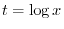
where
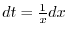
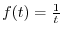 . Now
. Now  is even function and
is even function and
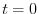 . Thus,
. Thus,
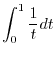
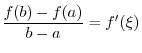 . Then
. Then 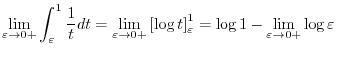 .
.
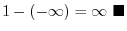 .
.
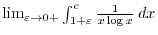 . Thus,
. Thus,
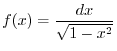
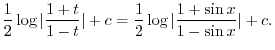 . Then
. Then
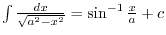 ,
,
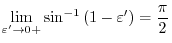 ,
,
 and
and
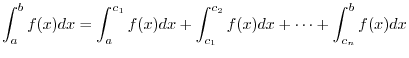 . Also,
. Also,
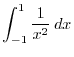 ,
,
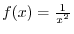 ,
,
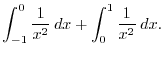 . Thus,
. Thus,
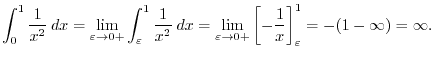
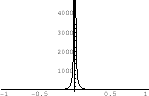
4. By 3.
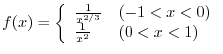 . We show
. We show
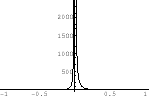 .
.
For  ,
,
 |
 |
![$\displaystyle \int_{0}^{\frac{\pi}{2}}\sin^{n-1}{x}\sin{x}dx = -\left[\sin^{n-1}{x}\cos{x}\right]_{0}^{\frac{\pi}{2}}$](img3183.png) |
|
 |
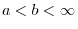 |
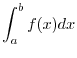 . Thus
. Thus
![$\left[\sin^{n-1}{x}\cos{x}\right]_{0}^{\frac{\pi}{2}} = 0$](img3186.png) . Now we take care of the rest.
. Now we take care of the rest.
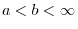 |
 |
 |
|
 |
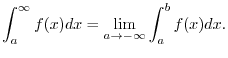 |
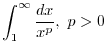 . Note
. Note
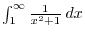 ,
,
 |
 |
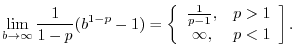 |
|
 |
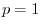 |
||
 |
 |
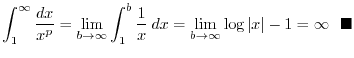 |
|
 |
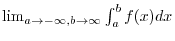 |
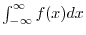
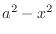 . Let
. Let
 and
and
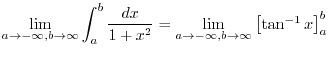 ,
,
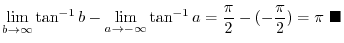 ,
,
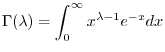 . Thus
. Thus
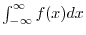

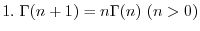

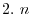
|
Exercise A
|
 ?D
?D
 be a continuous function on the interval
be a continuous function on the interval
 . Then answer the following question concerning the function
. Then answer the following question concerning the function
 ?D
?D
(a) Show that  is an odd function?D
is an odd function?D
(b) Show that  is even function implies that
is even function implies that 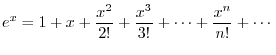 is an odd function.
is an odd function.
(c) Show that
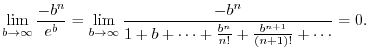 implies that
implies that 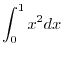 ?D
?D
(d) Show that  can be represented by a sum and a difference of functions?D
can be represented by a sum and a difference of functions?D