Next: Integration by Parts Up: Integration Previous: Antiderivatives Contents Index
| Integration by Substitution |
|---|
|
|
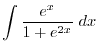 . Then
. Then
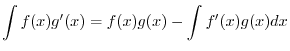 . If the integrand of a given integral is transformed to the known form of the Rules of integration, then we can solve the problem by integration by substitution..
. If the integrand of a given integral is transformed to the known form of the Rules of integration, then we can solve the problem by integration by substitution..
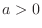 . Integrate the following functions
. Integrate the following functions
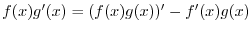 2.
2.
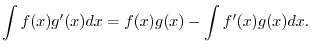 3.
3.
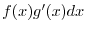
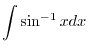 . Then
. Then
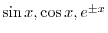 . Thus,
. Thus,
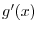
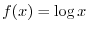
2. Let
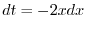 . Then
. Then
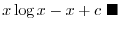 .
.
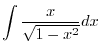 |
 |
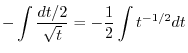 |
|
 |
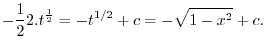 |
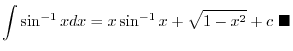 |
 |
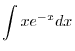 |
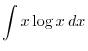 . Then
. Then
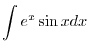 . Thus
. Thus
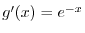 |
 |
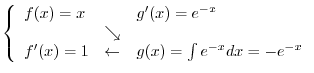 |
|
 |
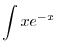 |
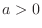 . Then integrate the following functions.
. Then integrate the following functions.
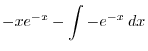 2.
2.
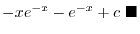
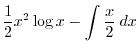 . Then
. Then 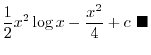 and
and 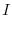 . Thus
. Thus
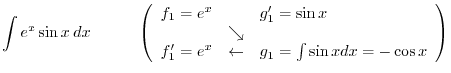 |
 |
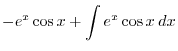 |
|
 |
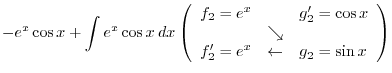 |
||
 |
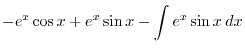 |
||
 |
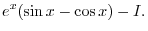 |
||
 |
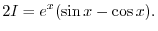 |
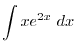 where
where
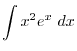 . Then
. Then
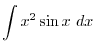 . Since
. Since
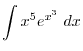 , we have
, we have
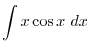
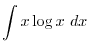 . Thus
. Thus
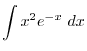
|
Exercise A
|
|
Exercise B
|