Integration by Parts

Integration by Parts

Theorem 3..5 Let 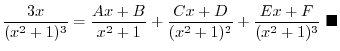be differentiable functions. Then.

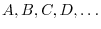
$\displaystyle \int f(x)g^{\prime}(x) = f(x)g(x) - \int f^{\prime}(x)g(x)dx$

NOTE . Then . Now integrate both sides with respect .

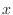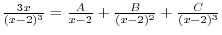
$\displaystyle \int f(x)g'(x)dx = f(x)g(x) - \int f'(x)g(x)dx.$
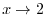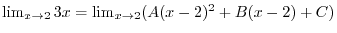If is hard to integrate, Rewrite by parts to get integration of $\int f(x)g'(x)dx$ .

Example 3..4 Integrate the following function by parts.
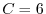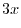
1. $\displaystyle{\int \log{x} dx}$ 2. $\displaystyle{\int \sin^{-1}{x}dx}$
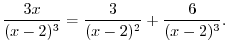
SOLUTION 1. $\left\{\begin{array}{lcl} f(x) = \log{x} & & g'(x) = 1\\ &\searrow& \\ f'(x) = \frac{1}{x} &\leftarrow& g(x) = \int dx = x \end{array}\right.$
Thus

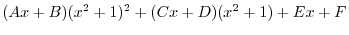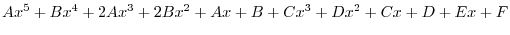$\displaystyle \int \underbrace{\log{x}}_{f} \underbrace{1}_{g'}dx$ $\displaystyle =$ $\displaystyle \underbrace{x}_{g} \underbrace{\log{x}}_{f} - \int \underbrace{x}_{g} \underbrace{\frac{1}{x}}_{f'} dx$

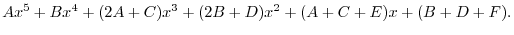$\displaystyle =$ $\displaystyle x \log{x} - x + c\ensuremath{\ \blacksquare}$

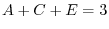
2. $\left\{\begin{array}{lcl} f(x) = \sin^{-1}{x} & & g'(x) = dx\\ &\searrow& \\... ...x) = \frac{1}{\sqrt{1-x^2}} &\leftarrow& g(x) = \int dx = x \end{array}\right.$
Thus

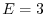
$\displaystyle \int \underbrace{\sin^{-1}{x}}_{f}\underbrace{dx}_{g'} = \underbr... ...}}_{f} - \int \underbrace{x}_{g} \underbrace{\frac{1}{\sqrt{1-x^{2}}}dx}_{f'}.$

Now let 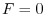. Then 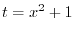. Thus

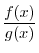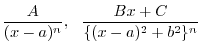$\displaystyle \int \frac{x}{\sqrt{1-x^{2}}}dx$ $\displaystyle =$ $\displaystyle -\int \frac{dt/2}{\sqrt{t}} = -\frac{1}{2}\int t^{-1/2} dt$

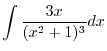$\displaystyle =$ $\displaystyle - \frac{1}{2}2. t^{\frac{1}{2}} = - t^{1/2} + c = - \sqrt{1 - x^2} + c.$

Thus,

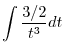
$\displaystyle \int \sin^{-1}{x} dx = x\sin^{-1}{x} + \sqrt{1 - x^{2}} + c\ensuremath{\ \blacksquare}$

Exercise 3..4 Integrate the following functions.
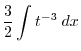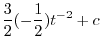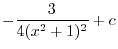
1. $\displaystyle{\int x e^{-x} dx}$ 2. $\displaystyle{\int x\log{x}\:dx}$ 3. $\displaystyle{\int e^{x}\sin{x}dx}$

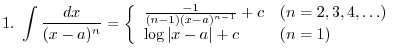
SOLUTION 1. $\left\{\begin{array}{lcl} f(x) = x & & g'(x) = e^{-x}\\ &\searrow& \\ f'(x) = 1 &\leftarrow& g(x) = \int e^{-x}dx = -e^{-x} \end{array}\right.$
Thus,

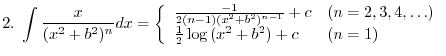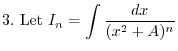$\displaystyle \int xe^{-x}$ $\displaystyle =$ $\displaystyle -xe^{-x} - \int -e^{-x}\: dx$

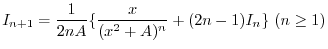$\displaystyle =$ $\displaystyle -xe^{-x} -e^{-x} + c\ensuremath{\ \blacksquare}$

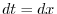
2. $\left\{\begin{array}{lcl} f(x) = \log{x} & & g'(x) = x\\ &\searrow& \\ f'(x) = \frac{1}{x} &\leftarrow& g(x) = \int xdx = \frac{x^2}{2} \end{array}\right.$
Thus,

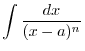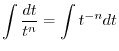$\displaystyle \int x\log{x}$ $\displaystyle =$ $\displaystyle \frac{1}{2}x^2 \log{x} - \int \frac{1}{x}\cdot \frac{x^2}{2}\: dx$

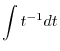$\displaystyle =$ $\displaystyle \frac{1}{2}x^2 \log{x} - \int \frac{x}{2}\: dx$

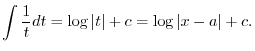$\displaystyle =$ $\displaystyle \frac{1}{2}x^2 \log{x} - \frac{x^2}{4} + c\ensuremath{\ \blacksquare}$

3.

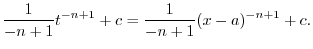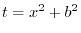$\displaystyle I$ $\displaystyle =$ $\displaystyle \int e^{x}\sin{x}\:dx \hskip 1cm \left(\begin{array}{lcl} f_1 = e... ... \\ f_1' = e^x &\leftarrow& g_1 = \int \sin{x}dx = -\cos{x} \end{array}\right)$

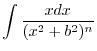$\displaystyle =$ $\displaystyle -e^{x} \cos{x} + \int e^{x} \cos{x}\:dx$

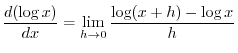Now the integral of the second tern is very similar to the original integral . So, we integrate again. .

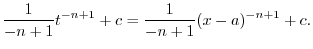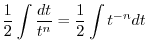$\displaystyle I$ $\displaystyle =$ $\displaystyle -e^{x} \cos{x} + \int e^{x} \cos{x}\:dx \left(\begin{array}{lcl} ... ...s{x}\\ &\searrow& \\ f_2' = e^x &\leftarrow& g_2 = \sin{x} \end{array}\right)$

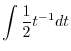$\displaystyle =$ $\displaystyle -e^{x}\cos{x} + e^{x}\sin{x} - \int e^x \sin{x}\:dx$

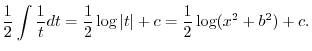$\displaystyle =$ $\displaystyle e^{x}(\sin{x} - \cos{x}) - I.$

Then,

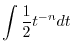
$\displaystyle 2I = e^{x}(\sin{x} - \cos{x}).$
Thus,

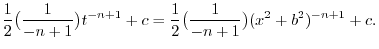
$\displaystyle I = \frac{1}{2}e^{x}(\sin{x} - \cos{x})\ensuremath{\ \blacksquare}$

Exercise A

1.

Work out the following integrals?D
(a) $\displaystyle{\int{xe^{x}}\ dx}$ (b) $\displaystyle{\int{x\sin{x}}\ dx}$ (c) $\displaystyle{\int{xe^{2x}}\ dx}$ (d) $\displaystyle{\int{x^{2}e^{x}}\ dx}$
(e) $\displaystyle{\int{x^{2}\sin{x}}\ dx}$ (f) $\displaystyle{\int{x^{5}e^{x^{3}}}\ dx}$ (g) $\displaystyle{\int{x\cos{x}}\ dx}$

Exercise B

1.
Work out the following integrals?D

(a) $\displaystyle{\int{x\log{x}}\ dx}$ (b) $\displaystyle{\int{x^2e^{-x}}\ dx}$ (c) $\displaystyle{\int{(\log{x})^2}\ dx}$

(d) $\displaystyle{\int{x(x+5)^{14}}\ dx}$ (e) $\displaystyle{\int{x^{2}\cos{x}}\ dx}$ (f) $\displaystyle{\int{e^{x}\sin{x}}\ dx}$
( is integer)
(g) $\displaystyle{\int{\log{(1+x^2)}}\ dx}$ (h) $\displaystyle{\int{x\tan^{-1}{x}}\ dx}$ (i) $\displaystyle{\int{x^n\log{x}}\ dx}$ n

(j) $\displaystyle{\int{x^3\sin{x}}\ dx}$ (k) $\displaystyle{\int{x\sinh{x}}\ dx}$

Next:Integration of Rational Functions Up:Integration Previous:Integration by Substitution Contents Index

$\displaystyle \int \underbrace{\log{x}}_{f} \underbrace{1}_{g'}dx$	$\displaystyle =$	$\displaystyle \underbrace{x}_{g} \underbrace{\log{x}}_{f} - \int \underbrace{x}_{g} \underbrace{\frac{1}{x}}_{f'} dx$
	$\displaystyle =$	$\displaystyle x \log{x} - x + c\ensuremath{\ \blacksquare}$

$\displaystyle \int \frac{x}{\sqrt{1-x^{2}}}dx$	$\displaystyle =$	$\displaystyle -\int \frac{dt/2}{\sqrt{t}} = -\frac{1}{2}\int t^{-1/2} dt$
	$\displaystyle =$	$\displaystyle - \frac{1}{2}2. t^{\frac{1}{2}} = - t^{1/2} + c = - \sqrt{1 - x^2} + c.$

$\displaystyle \int xe^{-x}$	$\displaystyle =$	$\displaystyle -xe^{-x} - \int -e^{-x}\: dx$
	$\displaystyle =$	$\displaystyle -xe^{-x} -e^{-x} + c\ensuremath{\ \blacksquare}$

$\displaystyle \int x\log{x}$	$\displaystyle =$	$\displaystyle \frac{1}{2}x^2 \log{x} - \int \frac{1}{x}\cdot \frac{x^2}{2}\: dx$
	$\displaystyle =$	$\displaystyle \frac{1}{2}x^2 \log{x} - \int \frac{x}{2}\: dx$
	$\displaystyle =$	$\displaystyle \frac{1}{2}x^2 \log{x} - \frac{x^2}{4} + c\ensuremath{\ \blacksquare}$

$\displaystyle I$	$\displaystyle =$	$\displaystyle \int e^{x}\sin{x}\:dx \hskip 1cm \left(\begin{array}{lcl} f_1 = e... ... \\ f_1' = e^x &\leftarrow& g_1 = \int \sin{x}dx = -\cos{x} \end{array}\right)$
	$\displaystyle =$	$\displaystyle -e^{x} \cos{x} + \int e^{x} \cos{x}\:dx$