Next: Integration by Substitution Up: Integration Previous: Integration Contents Index
| Primitive Functions |
|---|
Given a function  defined on some interval defined on some interval 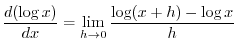 . Then a function . Then a function 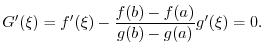 safisfies safisfies
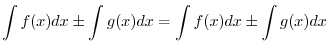 is called primitive function of is called primitive function of  . .
|
| Antiderivatives |
|---|
|
Theorem 3..1 Let
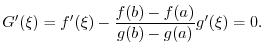 be a primitive function of be a primitive function of  . Then every primitive function of . Then every primitive function of  is given by is given by 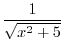 , where , where 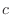 is an arbitrary constant. is an arbitrary constant. |
Proof
Let 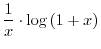 be a primitive function of
be a primitive function of  . Then
. Then
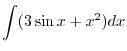 and since
and since
 ,
,
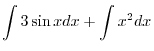 . Now let
. Now let
 . Then
. Then 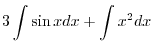 . This means that
. This means that
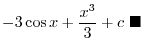 , where
, where 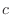 is constant. Thus
is constant. Thus
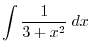 .
Note that
.
Note that
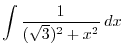

| Antiderivatives |
|---|
Every primitive function of  is called a antiderivative and denoted by is called a antiderivative and denoted by
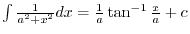 . .
|
 is calle antidifferentiation or integration.
is calle antidifferentiation or integration.
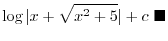
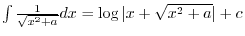 .
Then since the derivative of a sum is the sum of the derivatives,
.
Then since the derivative of a sum is the sum of the derivatives,
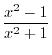
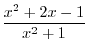
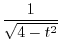
SOLUTION Note that
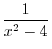
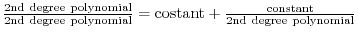
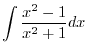
| Integration Formulas |
|---|
|
|
NOTE Differentiate the right-hand side to get the integrand.
1.
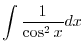 . Thus,
. Thus,
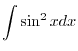
10.
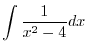 |
 |
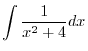 |
NOTE
Rules of Integration
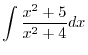

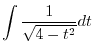

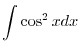
Thus,
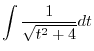
2.
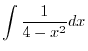
3.
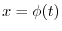
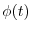
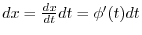 2.
2.
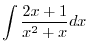 3.
3.
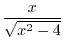
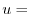 |
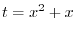 |
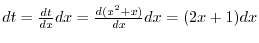 |
|
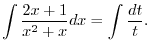 |
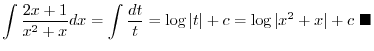 |
||
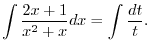 |
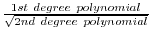 |
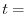 |
 |
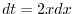 |
|
 |
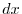 |
3.
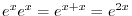 |
 |
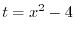 |
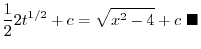 2.
2.
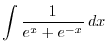 3.
3.
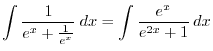 4.
4.
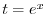
SOLUTION
1.
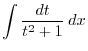 |
 |
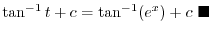 |
|
 |
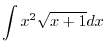 |
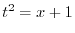 |
 |
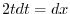 |
|
 |
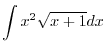 |
||
 |
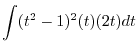 |
||
 |
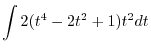 |
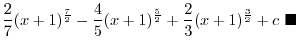 |
 |
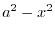 |
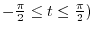 |
 |
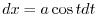 |
|
 |
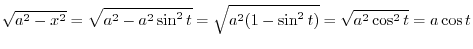 |
||
 |
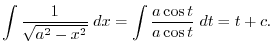 |
Alternative solution By the rule of the integration, we have
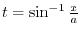
|
Exercise A
|
|
Exercise B
|