Next: Higher Order Derivatives Up: Differentiation Previous: Derivatives Contents Index
NOTE Denote Differentiation of Composite Functions
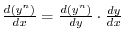 and
and 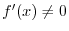 are differentiable as a function of
are differentiable as a function of 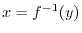 and
and  respectively, then the compostite function
respectively, then the compostite function
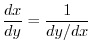 is differentiable as a function of
is differentiable as a function of  and
and
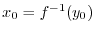
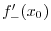 small change of
small change of  . Then
. Then 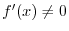 changes
changes
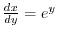 . Also,
. Also,
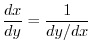 changes
changes
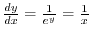 . Thus,
. Thus,
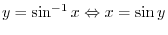 and
and
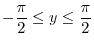
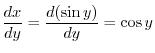 |
 |
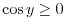 |
|
 |
 |
||
 |
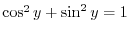 |
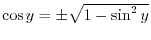 implies
implies
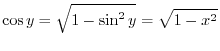 and
and
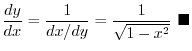 are differentiable, we have
are differentiable, we have
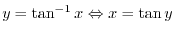
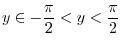
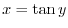 .
. 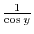 is a composite function of
is a composite function of
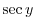 and
and
 . Thus
. Thus
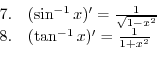
2. Suppose 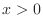 . Then
. Then
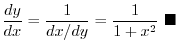 and
and
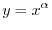 .
Suppose next that
.
Suppose next that 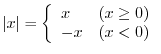 . Then
. Then 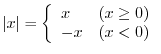 and
and 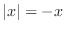 imply
imply
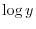 . Set
. Set 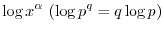 . Then ,
. Then ,
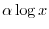
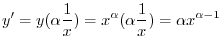 be integers. Differentiate the following
be integers. Differentiate the following
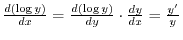
SOLUTION Raise both sides of the equation to the nth power.
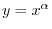
 . Then
. Then
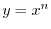
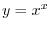
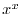
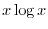
Proof
Let
Differentiation of Inverse Function
 is differentiable on some interval and
is differentiable on some interval and
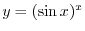 . If the inverse
. If the inverse
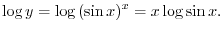 of
of 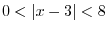 exists, then
exists, then
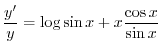
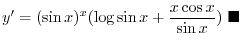 . Then
. Then
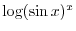
SOLUTION Note that
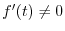 for the principal value is in
for the principal value is in
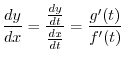 . Differentiate both sides of
. Differentiate both sides of
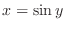 by
by  . Then
. Then
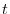
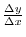 for
for
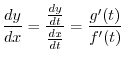 ,
,
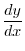
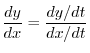
SOLUTION
Note that
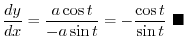 for the principal valueof
for the principal valueof
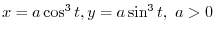 . Differentiate both sides of
. Differentiate both sides of
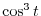 by
by  . Then
. Then
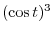
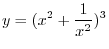
NOTE The name logarithmic differentiation comes from this process. We also note that the derivative of
Logarithmic Differentiation
To find the derivative of
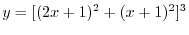 . We first take logarihtm to both sides. Then
. We first take logarihtm to both sides. Then
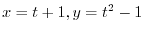

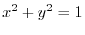
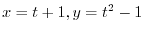

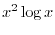
Next differentiate both sides to get
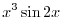
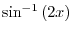
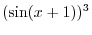 looks exactly the same as the derivative of
looks exactly the same as the derivative of 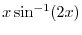 .
.
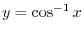 .
.
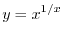
 .
.
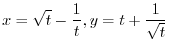
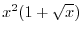
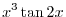 .
.
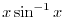
 .
.
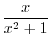
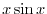
| Differentiation of Parametric Functions |
|---|
|
Theorem 2..5 Suppose that
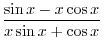 and and 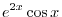 are differentiable on are differentiable on 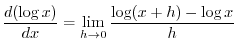 and and
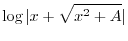 . Then . Then  is differentiable in is differentiable in  and the following is holds. and the following is holds.
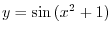
|
NOTE For a function 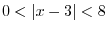 , the value of
, the value of  is determined by the value of
is determined by the value of  . If you want describe the behavior of ant on a table, you want to know the position of ant. To do this,
. If you want describe the behavior of ant on a table, you want to know the position of ant. To do this,  and
and  must be expressed using the time variable
must be expressed using the time variable 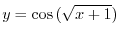 . Then we say
. Then we say 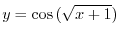 parameter. If
parameter. If  and
and  is given by
is given by 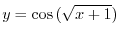 , then by the small change of
, then by the small change of 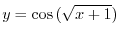 cause some change of
cause some change of  and
and  . The amount of change is given by
. The amount of change is given by  and
and  . Thus the rate of small change of
. Thus the rate of small change of  with respect to small change of
with respect to small change of  is given by
is given by
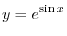 .
.
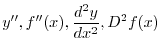 . Find
. Find
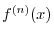 .
.
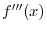
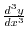 . Find
. Find
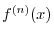 .
.
|
Exercise A
|
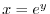
|
Exercise B
|
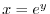 .
.