Next: Mean Value Theorem Up: Differentiation Previous: Differentiation Formnulas Contents Index
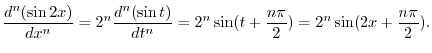 is continuous, we say
is continuous, we say  is class
is class 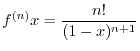 . Also, if for all
. Also, if for all  ,
,
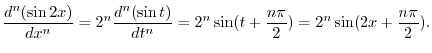 exist. Then
exist. Then  is called infinitely differentiable or class
is called infinitely differentiable or class
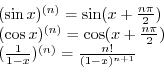 .
.
Properties of Higher Order Derivatives
Theorem 2..6 Suppose that
 and
and 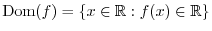 are in class
are in class 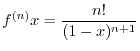 and
and 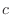 is constant. Then we have the following.
is constant. Then we have the following.
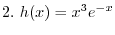
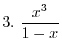
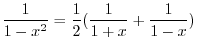
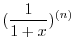
NOTE
The theorem 3. is called general Leibnitz rule.
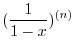
Proof of 3. Use induction on  . For
. For 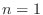 , we have
, we have
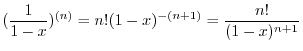
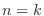 and consider for
and consider for 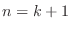 .
.
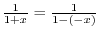 |
 |
![$\displaystyle [(f(x)g(x))^{(k)}]^{\prime} = [ \sum_{i=0}^{k}\binom{k}{i}f^{(k-i)}(x)g^{(i)}(x)]^{\prime}$](img1687.png) |
 |
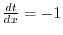 |
||
 |
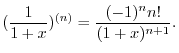 |
||
 |
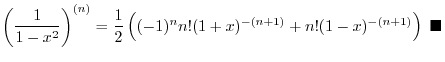 |
||
 |
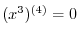 |
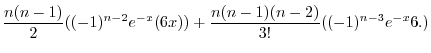
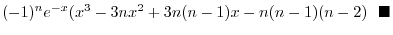 . Then
. Then
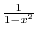 . Thus true for
. Thus true for 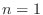 . Now assume true for
. Now assume true for 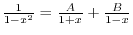 and consider for
and consider for  .
.
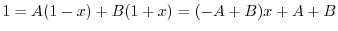 |
 |
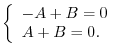 |
|
 |
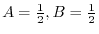 |
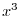
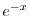
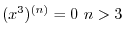
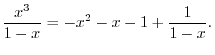
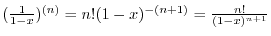 by induction
by induction

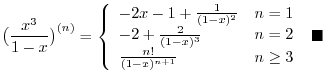 . Then
. Then
 . Thus,
. Thus,
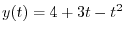
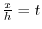 |
 |
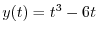 |
|
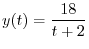 |
 |
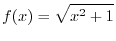 |
|
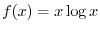 |
 |
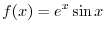 |
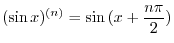 by induction
by induction

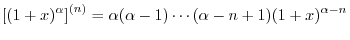
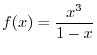
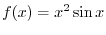
SOLUTION 1. Using the partial fraction, to write
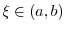
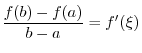 and
and
 .
.
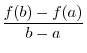
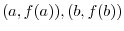 . Put
. Put 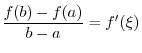 . Then
. Then
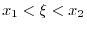 . Thus,
. Thus,
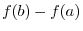
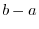
2. Note that
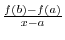 . Thus we let
. Thus we let
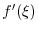 and
and
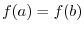 and use general Leibnitz rule,
and use general Leibnitz rule,
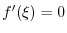 |
 |
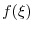 |
|
 |
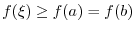 |
||
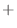 |
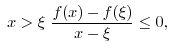 |
||
 |
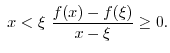 |
3. Since the degree of the numerator
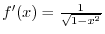 the degree of the denominator, divide the numerator by the denominator.
the degree of the denominator, divide the numerator by the denominator.
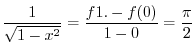
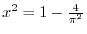 , we have
, we have
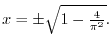
|
Exercise A
|
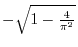 ?D
?D
|
Exercise B
|
 -th derivative of the following functions.
-th derivative of the following functions.