Next: 7.6 Answer Up: MULTIPLE INTEGRATION Previous: 7.5 Answer Ź§ł°
|
Exercise
|
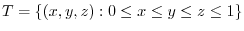 üCevaluate the following triple integrals.
üCevaluate the following triple integrals.
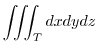
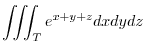
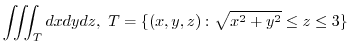
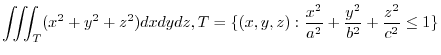
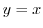 and
and
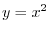 with the constant density.
with the constant density.
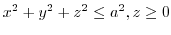 with the density proportional to the distance from the center.
with the density proportional to the distance from the center.
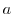 and the height
and the height 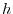 with constant density.
with constant density.
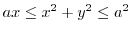 .
.
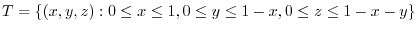 . Find
. Find
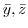
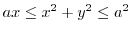 with the density is proportional to the distance from the origin.
with the density is proportional to the distance from the origin.