Next: 索引 Up: MULTIPLE INTEGRATION Previous: Triple integrals 索引
7.6
1.
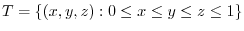
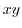 -plane. Then
-plane. Then
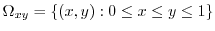
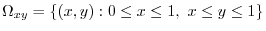
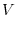 |
 |
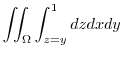 |
|
 |
![$\displaystyle \int_{x=0}^{1}\int_{x}^{1} [z]_{y}^{1}dy dx$](img969.png) |
||
 |
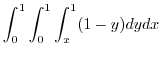 |
||
 |
![$\displaystyle \int_{0}^{1}\left[y - \frac{y^2}{2}\right]_{x}^{1} dx$](img971.png) |
||
 |
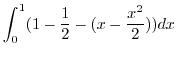 |
||
 |
![$\displaystyle \left[\frac{x}{2} - \frac{x^2}{2} + \frac{x^3}{6}\right]_{0}^{1}$](img973.png) |
||
 |
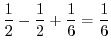 |
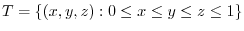
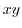 -plane.
-plane.
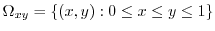
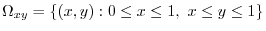
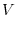 |
 |
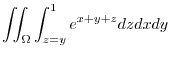 |
|
 |
![$\displaystyle \int_{x=0}^{1}\int_{x}^{1} [e^{x+y+z}]_{y}^{1}dy dx$](img976.png) |
||
 |
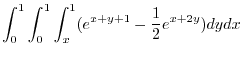 |
||
 |
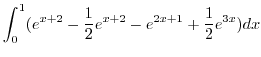 |
||
 |
![$\displaystyle \left[\frac{1}{2}e^{x+2} - \frac{1}{2}e^{2x+1} + \frac{1}{6}e^{3x}\right]_{0}^{1}$](img979.png) |
||
 |
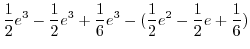 |
||
 |
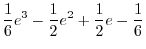 |
||
 |
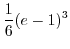 |
2.
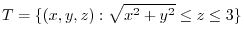
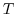 is bounded by the upper semisphere
is bounded by the upper semisphere
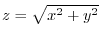 and the plane
and the plane 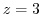 .Also,the line of intersection of
.Also,the line of intersection of
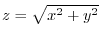 and
and 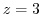 is
is
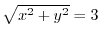 .Thus,
.Thus,
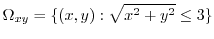
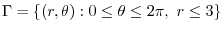
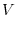 |
 |
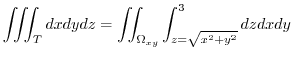 |
|
 |
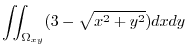 |
||
 |
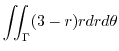 |
||
 |
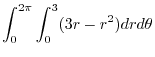 |
||
 |
![$\displaystyle \int_{0}^{2\pi}\left[\frac{3r^2}{2} - \frac{r^3}{3}\right]_{0}^{3} d\theta$](img994.png) |
||
 |
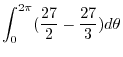 |
||
 |
![$\displaystyle \frac{27}{6}[\theta]_{0}^{2\pi} = 9\pi$](img996.png) |
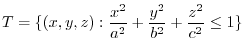
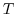 is an ellipsoid.To be able to use the shperical coordinatess, we use the following change of variable.
is an ellipsoid.To be able to use the shperical coordinatess, we use the following change of variable.
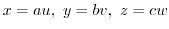
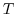 is transfered to
is transfered to
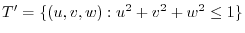 .Then
.Then
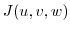 |
 |
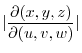 |
|
 |
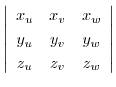 |
||
 |
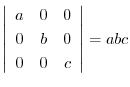 |
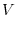 |
 |
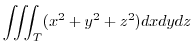 |
|
 |
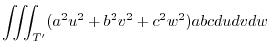 |
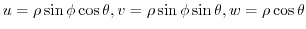
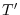 maps to
maps to
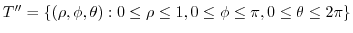
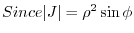 ,
,
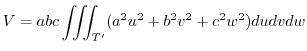
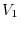 |
 |
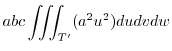 |
|
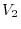 |
 |
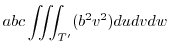 |
|
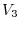 |
 |
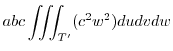 |
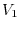 . Then
. Then
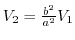 ,
,
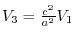 .
.
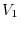 |
 |
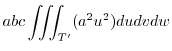 |
|
 |
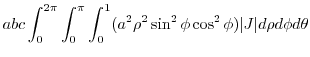 |
||
 |
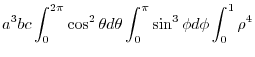 |
||
 |
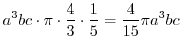 |
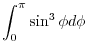 |
 |
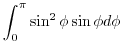 |
|
 |
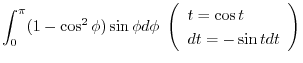 |
||
 |
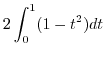 |
||
 |
![$\displaystyle 2\left[t - \frac{t^3}{3} \right]_{0}^{1} = \frac{4}{3}$](img1027.png) |
3.
(a) Let the 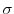 be density. Then
be density. Then 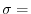 constant.
constant.
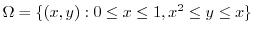
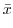 |
 |
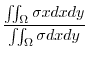 |
|
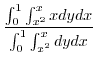 |
|||
 |
![$\displaystyle \frac{\int_{0}^{1}[xy]_{x^2}^{x}dx}{\int_{0}^{1}[y]_{x^2}^{x}dx}$](img1033.png) |
||
 |
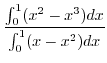 |
||
 |
![$\displaystyle \frac{\left[\frac{x^3}{3} - \frac{x^4}{4}\right]_{0}^{1}}{\left[\frac{x^2}{2} - \frac{x^3}{3}\right]_{0}^{1}}$](img1035.png) |
||
 |
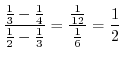 |
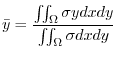
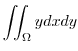 |
 |
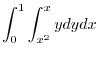 |
|
 |
![$\displaystyle \int_{0}^{1}\left[\frac{y^2}{2}\right]_{x^2}^{x}dx$](img1040.png) |
||
 |
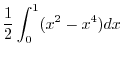 |
||
 |
![$\displaystyle \frac{1}{2}\left[\frac{x^3}{3} - \frac{x^5}{5}\right]_{0}^{1}$](img1042.png) |
||
 |
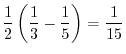 |
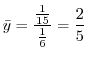
(b)
By symmetry,
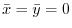 .Let
.Let  be the density.
be the density.
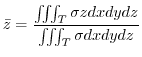
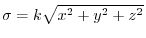 .Express
.Express
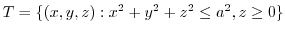
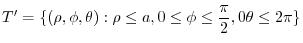
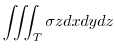 |
 |
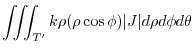 |
|
 |
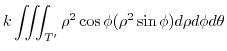 |
||
 |
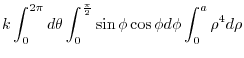 |
||
 |
![$\displaystyle 2k\pi \left[\frac{\sin^{2}{\phi}}{2}\right]_{0}^{\frac{\pi}{2}} \left[\frac{\rho^5}{5}\right]_{0}^{a}$](img1054.png) |
||
 |
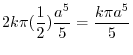 |
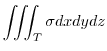 |
 |
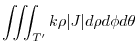 |
|
 |
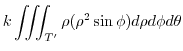 |
||
 |
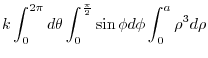 |
||
 |
![$\displaystyle 2k\pi \left[-\cos{\phi}\right]_{0}^{\frac{\pi}{2}} \left[\frac{\rho^4}{4}\right]_{0}^{a}$](img1060.png) |
||
 |
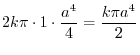 |
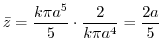
(c)
The right circular cone 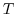 with the radius
with the radius 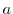 and the height
and the height 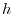 is expressed by
is expressed by
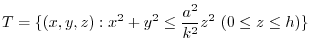
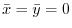 .
.
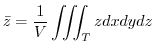
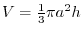 .
Express
.
Express 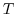 using the cylindrical coordinates. Then
using the cylindrical coordinates. Then
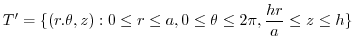
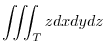 |
 |
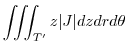 |
|
 |
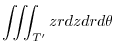 |
||
 |
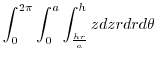 |
||
 |
![$\displaystyle \int_{0}^{2\pi}\int_{0}{a}\left[\frac{z^2}{2}\right]_{\frac{hr}{a}}^{h} r dr d\theta$](img1071.png) |
||
 |
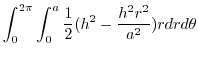 |
||
 |
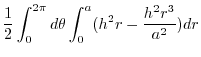 |
||
 |
![$\displaystyle \pi\left[\frac{h^2 r^2}{2} - \frac{h^2 a^4}{4a^2}\right]_{0}^{a}d\theta$](img1074.png) |
||
 |
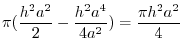 |
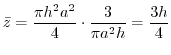
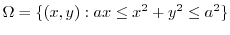
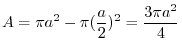
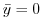 .Now using the porlarcoordinates
.Now using the porlarcoordinates 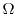 を表わすと
を表わすと
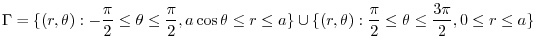
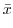 |
 |
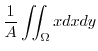 |
|
 |
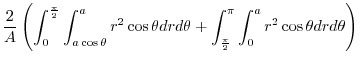 |
||
 |
![$\displaystyle \frac{2}{A} \left(\int_{0}^{\frac{\pi}{2}}\left[\frac{r^3 \cos{\t...
...rac{\pi}{2}}^{\pi}\left[\frac{r^3 \cos{\theta}}{3}\right]_{0}^{a}d\theta\right)$](img1084.png) |
||
 |
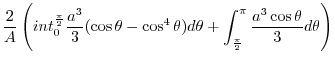 |
||
 |
![$\displaystyle \frac{2}{A}\left(\frac{a^3}{3}(1 - \frac{3\cdot 1}{4\cdot2}\frac{\pi}{2}) + \left[\frac{a^3\sin{\theta}}{3}\right]_{\frac{\pi}{2}}^{\pi}\right)$](img1086.png) |
||
 |
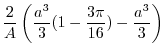 |
||
 |
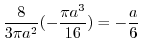 |
(e)
To evaluate the triple interal, project 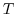 onto the appropriate axes plane.Here project
onto the appropriate axes plane.Here project 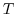 to
to 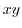 plane.Using V-simple,
plane.Using V-simple,
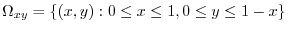
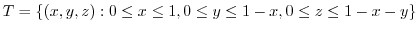
 |
 |
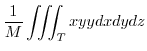 |
|
 |
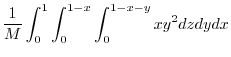 |
||
 |
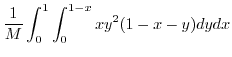 |
||
 |
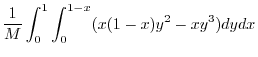 |
||
 |
![$\displaystyle \frac{1}{M}\int_{0}^{1}\left[\frac{x(1-x)y^{3}}{3} - \frac{xy^{4}}{4})\right ]_{0}^{1-x}dx$](img1096.png) |
||
 |
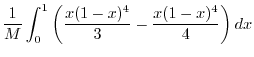 |
||
 |
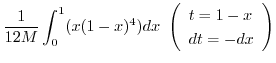 |
||
 |
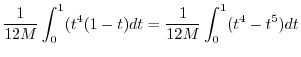 |
||
 |
![$\displaystyle \frac{1}{12M}\left[\frac{t^5}{5} - \frac{t^6}{6}\right]_{0}^{1} = \frac{1}{360M}$](img1100.png) |
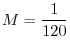 implies
implies
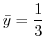 .
Also,
.
Also,
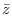 |
 |
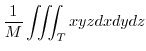 |
|
 |
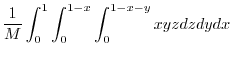 |
||
 |
![$\displaystyle \frac{1}{M}\int_{0}^{1}\int_{0}^{1-x}\left[\frac{xyz^2}{2}\right]_{0}^{1-x-y}dydx$](img1106.png) |
||
 |
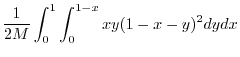 |
||
 |
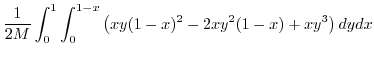 |
||
 |
![$\displaystyle \frac{1}{2M}\int_{0}^{1}\left[\frac{x(1-x)^2 y^{2}}{2} - \frac{2x(1-x)y^{3}}{3}) + \frac{xy^4}{4}\right ]_{0}^{1-x}dx$](img1109.png) |
||
 |
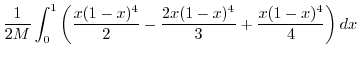 |
||
 |
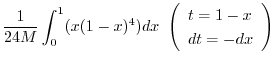 |
||
 |
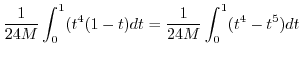 |
||
 |
![$\displaystyle \frac{1}{24M}\left[\frac{t^5}{5} - \frac{t^6}{6}\right]_{0}^{1} = \frac{1}{720M}$](img1113.png) |
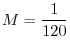 implies
implies
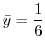 .
.
(f) The density  is proportional to the distance from the origin. Then,
is proportional to the distance from the origin. Then,
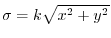 .Also,the mass
.Also,the mass 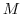 of
of
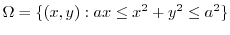
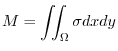
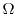 . Then
. Then
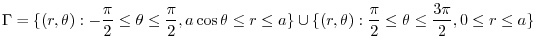
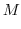 |
 |
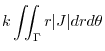 |
|
 |
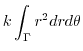 |
||
 |
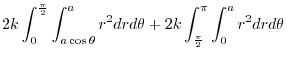 |
||
 |
![$\displaystyle 2k\int_{0}^{\frac{\pi}{2}}\left[\frac{r^3}{3}\right]_{a\cos{\thet...
...d\theta + 2k\int_{\frac{\pi}{2}}^{\pi}\left[\frac{r^3}{3}\right]_{0}^{a}d\theta$](img1122.png) |
||
 |
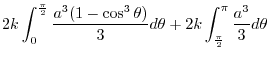 |
||
 |
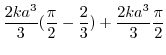 |
||
 |
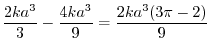 |
By the symmetry,
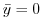 .Thus
.Thus
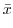 |
 |
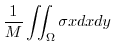 |
|
 |
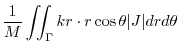 |
||
 |
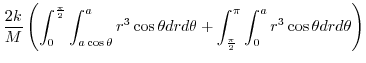 |
||
 |
![$\displaystyle \frac{2k}{M} \left(\int_{0}^{\frac{\pi}{2}}\left[\frac{r^4 \cos{\...
...rac{\pi}{2}}^{\pi}\left[\frac{r^4 \cos{\theta}}{4}\right]_{0}^{a}d\theta\right)$](img1129.png) |
||
 |
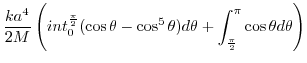 |
||
 |
![$\displaystyle \frac{ka^4}{2M}\left(1 - \frac{4\cdot 2}{5\cdot3\cdot 1} + \left[\sin{\theta}\right]_{\frac{\pi}{2}}^{\pi}\right)$](img1131.png) |
||
 |
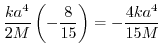 |
||
 |
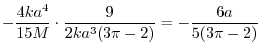 |